El algoritmo Parks-McClellan , publicado por James McClellan y Thomas Parks en 1972, es un algoritmo iterativo para encontrar el filtro de respuesta de impulso finito (FIR) óptimo de Chebyshev . El algoritmo Parks-McClellan se utiliza para diseñar e implementar filtros FIR eficientes y óptimos. Utiliza un método indirecto para encontrar los coeficientes de filtro óptimos.
El objetivo del algoritmo es minimizar el error en las bandas de pase y parada utilizando la aproximación de Chebyshev. El algoritmo Parks-McClellan es una variación del algoritmo de intercambio Remez , con el cambio de que está diseñado específicamente para filtros FIR. Se ha convertido en un método estándar para el diseño de filtros FIR.
En la década de 1960, los investigadores del campo del diseño de filtros analógicos utilizaban la aproximación de Chebyshev para el diseño de filtros. Durante este tiempo, era bien sabido que los mejores filtros contienen una característica equivalente en su magnitud de respuesta de frecuencia y el filtro elíptico (o filtro de Cauer) era óptimo con respecto a la aproximación de Chebyshev. Cuando comenzó la revolución de los filtros digitales en la década de 1960, los investigadores utilizaron una transformada bilineal para producir filtros elípticos digitales de respuesta de impulso infinito (IIR). También reconocieron el potencial del diseño de filtros FIR para realizar la misma tarea de filtrado y pronto se inició la búsqueda del filtro FIR óptimo utilizando la aproximación de Chebyshev. [1]
Era bien sabido tanto en matemáticas como en ingeniería que la respuesta óptima exhibiría un comportamiento equivalente a ondas y que el número de ondas podía contarse utilizando la aproximación de Chebyshev. En el período comprendido entre 1962 y 1971 se llevaron a cabo varios intentos de producir un programa de diseño para el filtro FIR Chebyshev óptimo. [1] A pesar de los numerosos intentos, la mayoría no tuvo éxito, generalmente debido a problemas en la implementación algorítmica o en la formulación del problema. Otto Herrmann, por ejemplo, propuso un método para diseñar filtros equivalentes con bordes de banda restringidos. [1] Este método obtuvo una respuesta de frecuencia equivalente a ondulaciones con el número máximo de ondulaciones resolviendo un conjunto de ecuaciones no lineales. Otro método introducido en ese momento implementó una aproximación óptima de Chebyshev, pero el algoritmo se limitó al diseño de filtros de orden relativamente bajo. [1]
De manera similar al método de Herrmann, Ed Hofstetter presentó un algoritmo que diseñaba filtros FIR con tantas ondulaciones como fuera posible. Esto se conoce como el algoritmo Maximal Ripple. El algoritmo Maximal Ripple impuso una condición de error alterno mediante interpolación y luego resolvió un conjunto de ecuaciones que la solución alterna tenía que satisfacer. [1] Una limitación notable del algoritmo Maximal Ripple fue que los bordes de la banda no se especificaron como entradas para el procedimiento de diseño. Más bien, el conjunto de frecuencia inicial { ω i } y la función deseada D ( ω i ) definieron implícitamente la banda de paso y parada. A diferencia de intentos anteriores de diseñar un filtro óptimo, el algoritmo Maximal Ripple utilizó un método de intercambio que intentaba encontrar el conjunto de frecuencias { ω i } donde el mejor filtro tenía sus ondulaciones. [1] Por lo tanto, el algoritmo Maximal Ripple no era un diseño de filtro óptimo, pero tuvo un impacto bastante significativo en cómo se formularía el algoritmo Parks-McClellan.
En agosto de 1970, James McClellan ingresó a la escuela de posgrado en la Universidad Rice con especialización en modelos matemáticos de diseño de filtros analógicos y se inscribió en un nuevo curso llamado "Filtros digitales" debido a su interés en el diseño de filtros. [1] El curso fue impartido conjuntamente por Thomas Parks y Sid Burrus . En ese momento, DSP era un campo emergente y, como resultado, las conferencias a menudo incluían artículos de investigación publicados recientemente. El semestre siguiente, la primavera de 1971, Thomas Parks ofreció un curso llamado "Teoría de la señal", que McClellan también tomó. [1] Durante las vacaciones de primavera del semestre, Parks condujo desde Houston a Princeton para asistir a una conferencia, donde escuchó la presentación de Ed Hofstetter sobre un nuevo algoritmo de diseño de filtro FIR (algoritmo Maximal Ripple). Trajo el artículo de Hofstetter, Oppenheim y Siegel a Houston, pensando en la posibilidad de utilizar la teoría de aproximación de Chebyshev para diseñar filtros FIR. [1] Escuchó que el método implementado en el algoritmo de Hofstetter era similar al algoritmo de intercambio de Remez y decidió seguir el camino del uso del algoritmo de intercambio de Remez. Los estudiantes del curso "Teoría de la señal" debían realizar un proyecto y, dado que la aproximación de Chebyshev era un tema importante en el curso, la implementación de este nuevo algoritmo se convirtió en el proyecto del curso de James McClellan. Esto finalmente condujo al algoritmo de Parks-McClellan, que implicaba la teoría de la aproximación óptima de Chebyshev y una implementación eficiente. A finales del semestre de primavera, McClellan y Parks intentaban escribir una variación del algoritmo de intercambio Remez para filtros FIR. El desarrollo llevó unas seis semanas y a finales de mayo se habían diseñado con éxito algunos filtros óptimos.
El algoritmo Parks-McClellan se implementa mediante los siguientes pasos: [1]
El algoritmo de Parks-McClellan se puede reformular en los siguientes pasos: [2]
Para obtener una comprensión básica del algoritmo de Parks-McClellan mencionado anteriormente, podemos reescribir el algoritmo anterior en una forma más simple como:
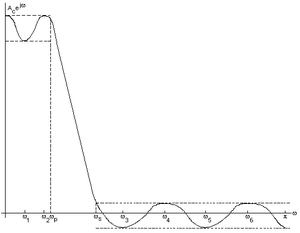
La imagen de arriba a la derecha muestra las diversas frecuencias extremas para el gráfico que se muestra. Las frecuencias extremas son los puntos máximo y mínimo en las bandas de parada y paso. La onda de la banda de parada es la porción inferior de las ondas en la parte inferior derecha del gráfico y la onda de la banda de paso es la porción superior de las ondas en la parte superior izquierda del gráfico. Las líneas discontinuas que atraviesan el gráfico indican el δ o error máximo. Dadas las posiciones de las frecuencias extremas, existe una fórmula para el δ óptimo o error óptimo. Como no conocemos el δ óptimo o las posiciones exactas de los extremos en el primer intento, iteramos. Efectivamente, asumimos inicialmente las posiciones de los extremos y calculamos δ. Luego reestimamos y movemos los extremos y recalculamos δ, o el error. Repetimos este proceso hasta que δ deje de cambiar. El algoritmo hará que el error δ converja, generalmente dentro de diez a doce iteraciones. [3]
Antes de aplicar la aproximación de Chebyshev, fueron necesarios una serie de pasos:
Dado que los filtros FIR podrían reducirse al caso de la suma de cosenos, se podría usar el mismo programa central para realizar todos los filtros FIR de fase lineal posibles. A diferencia del enfoque de máxima ondulación, los bordes de la banda ahora se pueden especificar con anticipación.
Para lograr una implementación eficiente del diseño de filtro óptimo utilizando el algoritmo de Parks-McClellan, se deben superar dos dificultades:
En cierto sentido, la programación implicó la implementación y adaptación de un algoritmo conocido para su uso en el diseño de filtros FIR. Se tomaron dos caras de la estrategia de intercambio para hacer más eficiente el programa:
En la inicialización, el número de extremos en la banda de paso y parada podría asignarse utilizando la relación de los tamaños de las bandas. Además, el borde de las bandas de paso y parada siempre se colocaría en el conjunto extremo, y la lógica del programa mantenía esas frecuencias de borde en el conjunto extremo. El movimiento entre bandas se controló comparando el tamaño de los errores en todas las frecuencias extremas candidatas y tomando la mayor. El segundo elemento del algoritmo fue el paso de interpolación necesario para evaluar la función de error. Utilizaron un método llamado forma baricéntrica de interpolación de Lagrange, que era muy robusto.
Todas las condiciones para el algoritmo de Parks-McClellan se basan en el teorema de alternancia de Chebyshev. El teorema de alternancia establece que el polinomio de grado L que minimiza el error máximo tendrá al menos L+2 extremos. La respuesta de frecuencia óptima apenas alcanzará los límites máximos de ondulación. [3] Los extremos deben ocurrir en los bordes de la banda de paso y parada y en ω=0 o ω=π o ambos. La derivada de un polinomio de grado L es un polinomio de grado L−1, que puede ser cero como máximo en L−1 lugares. [3] Entonces, el número máximo de extremos locales es el extremo local L−1 más los 4 bordes de la banda, dando un total de L+3 extremos.
Los siguientes enlaces adicionales proporcionan información sobre el algoritmo Parks-McClellan, así como sobre otras investigaciones y artículos escritos por James McClellan y Thomas Parks: