Lucid es un lenguaje de programación de flujo de datos diseñado para experimentar con modelos de programación distintos de von Neumann . Fue diseñado por Bill Wadge y Ed Ashcroft y descrito en el libro Lucid, the Dataflow Programming Language de 1985. [ 1 ]
pLucid fue el primer intérprete de Lucid.
Lucid utiliza un modelo basado en la demanda para el cálculo de datos. Cada enunciado puede entenderse como una ecuación que define una red de procesadores y líneas de comunicación entre ellos a través de las cuales fluyen los datos. Cada variable es un flujo infinito de valores y cada función es un filtro o un transformador. La iteración se simula mediante los valores "actuales" y el operador "fby" (que se lee como "seguido de"), que permite la composición de flujos.
Lucid se basa en un álgebra de historias, en la que una historia es una secuencia infinita de elementos de datos. En términos operativos, una historia puede considerarse como un registro de los valores cambiantes de una variable; las operaciones de historia, como primero y siguiente, pueden entenderse de maneras sugeridas por sus nombres. Lucid fue concebido originalmente como un lenguaje disciplinado, matemáticamente puro y de una sola asignación, en el que la verificación se simplificaría. Sin embargo, la interpretación del flujo de datos ha tenido una influencia importante en la dirección en la que Lucid ha evolucionado.[1]
En Lucid (y otros lenguajes de flujo de datos ), una expresión que contiene una variable que aún no se ha vinculado espera hasta que se haya vinculado la variable antes de continuar. Una expresión como x + yesperará hasta que tanto x como y estén vinculados antes de regresar con el resultado de la expresión. Una consecuencia importante de esto es que se evita la lógica explícita para actualizar valores relacionados, lo que da como resultado una reducción sustancial del código, en comparación con los lenguajes convencionales.
Cada variable en Lucid es un flujo de valores. Una expresión n = 1 fby n + 1define un flujo utilizando el operador 'fby' (una regla mnemotécnica para "seguido de"). fby define lo que viene después de la expresión anterior. (En este caso, el flujo produce 1,2,3,...). Los valores de un flujo pueden ser direccionados por estos operadores (suponiendo que x es la variable que se utiliza):
'first x'- obtiene el primer valor en el flujo x,
'x'- el valor actual del flujo,
'next x'- obtiene el siguiente valor en la secuencia.
'asa'- un operador que hace algo 'tan pronto como' la condición dada se vuelve verdadera.
'x upon p'- upon es un operador que repite el valor anterior del flujo x, y se actualiza a los nuevos valores solo cuando el flujo p pone un truevalor a disposición. (Sirve para ralentizar el flujo x) es decir: x upon pes el flujo x con nuevos valores que aparecen cuando p es verdadero.
El cálculo se lleva a cabo definiendo filtros o funciones de transformación que actúan sobre estos flujos de datos que varían en el tiempo.
cara dónde n = 0 por (n + 1); fac = 1 fby ( fac * (n + 1) ); fin
mentira dónde fib = 0 fby ( 1 fby fib + siguiente fib ); fin
total dónde total = 0 por total + x fin;
promedio_de_ejecución dónde suma = primero(entrada) fby suma + siguiente(entrada); n = 1 por n + 1; promedio_de_ejecución = suma / n; fin;
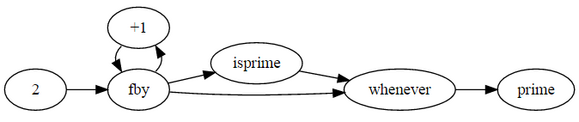
principal dónde primo = 2 fby (n siempre que sea primo (n)); n = 3 por n+1; es primo(n) = no(divs) como divs o primo*primo > N dónde N es la corriente n; divs = N mod primo eq 0; fin; fin
qsort(a) = si eof(primero a) entonces a de lo contrario sigue(qsort(b0),qsort(b1)) fi dónde p = primero a < a; b0 = a siempre que p; b1 = a siempre que no sea p; seguir(x,y) = si xhecho entonces y sobre xhecho de lo contrario x fi dónde xdone = iseod x fpor xdone o iseod x; fin fin
--------> siempre que -----> qsort --------- | ^ | | | | | no | | ^ | |---> primero | | | | | | | V | | |---> menos --- | | | | | VV---+--------> siempre que -----> qsort -----> conc -------> ifthenelse -----> | ^ ^ | | | --------> siguiente ----> primero ------> iseod -------------- | | | -------------------------------------------------- ---------
raíz cuadrada(promedio(cuadrado(a))) dónde cuadrado(x) = x*x; avg(y) = media dónde n = 1 por n+1; media = primera y fby media + d; d = (próximo y - media)/(n+1); fin; raíz cuadrada (z) = aprox. asa err < 0,0001 dónde Z es la corriente z; aprox = Z/2 fby (aprox + Z/aprox)/2; err = abs(cuadrado(aprox)-Z); fin; fin
yo dónde h = 1 por fusionar(fusionar(2 * h, 3 * h), 5 * h); fusionar(x,y) = si xx <= yy entonces xx de lo contrario yy fi dónde xx = x sobre xx <= yy; yy = y sobre yy <= xx; fin; fin;