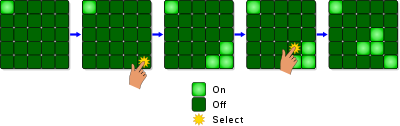
Lights Out es un juego electrónico lanzado por Tiger Electronics en 1995. [1] El juego consiste en una cuadrícula de luces de 5 por 5. Cuando comienza el juego, se enciende un número aleatorio o un patrón almacenado de estas luces. Al presionar cualquiera de las luces, esta y las luces adyacentes se encenderán. El objetivo del rompecabezas es apagar todas las luces, preferiblemente presionando la menor cantidad de botones posible. [1] [2]
Merlin , un juego electrónico similar, fue lanzado por Parker Brothers en la década de 1970 con reglas similares en una cuadrícula de 3x3. Otro juego similar fue producido por Vulcan Electronics en 1983 bajo el nombre de XL-25 . Tiger Toys también produjo una versión en cartucho de Lights Out para su consola de juegos portátil Game com en 1997, enviada gratis con la consola. Se han lanzado varios rompecabezas nuevos similares a Lights Out , como Lights Out 2000 (5x5 con múltiples colores), Lights Out Cube (seis caras de 3x3 con efectos en los bordes) y Lights Out Deluxe (6x6). [1] [2]
Lights Out fue creado por un grupo de personas entre las que se encontraban Avi Olti, Gyora Benedek, Zvi Herman, Revital Bloomberg, Avi Weiner y Michael Ganor. Los miembros del grupo, tanto en conjunto como de forma individual, también inventaron otros juegos, como Hidato , NimX, iTop y muchos más.

El juego consiste en una cuadrícula de luces de 5 x 5. Cuando comienza el juego, se enciende un número aleatorio o un patrón almacenado de estas luces. Al presionar cualquiera de las luces, esta y las cuatro luces adyacentes se encenderán. El objetivo del rompecabezas es apagar todas las luces, preferiblemente con la menor cantidad de pulsaciones de botones posible. [1] [4]
Si una luz está encendida, se debe pulsar un número impar de veces para que se apague. Si una luz está apagada, se debe pulsar un número par de veces (incluida ninguna) para que permanezca apagada. Se utilizan varias conclusiones para la estrategia del juego. En primer lugar, el orden en que se pulsan las luces no importa, ya que el resultado será el mismo. [5] En segundo lugar, en una solución mínima, cada luz no debe pulsarse más de una vez, porque pulsar una luz dos veces equivale a no pulsarla en absoluto. [5]
En 1998, Marlow Anderson y Todd Feil utilizaron álgebra lineal para demostrar que no todas las configuraciones son solucionables y también para demostrar que hay exactamente cuatro escenarios ganadores, sin incluir movimientos redundantes, para cualquier problema solucionable de 5 × 5. [6] La cuadrícula de 5 × 5 de Lights Out se puede representar como un vector de columna de 25 × 1 con un 1 y un 0 que significan una luz en su estado encendido y apagado respectivamente. Cada entrada es un elemento de Z 2 , el cuerpo de números enteros módulo 2. Anderson y Feil descubrieron que para que una configuración sea solucionable (derivando el vector nulo de la configuración original) debe ser ortogonal a los dos vectores N 1 y N 2 a continuación (representados como una matriz de 5 × 5 pero que no deben confundirse con matrices).
Además, descubrieron que N 1 y N 2 se pueden utilizar para encontrar tres soluciones adicionales a partir de una solución, y que estas cuatro soluciones son las únicas cuatro soluciones (excluyendo los movimientos redundantes) para la configuración inicial dada. Estas cuatro soluciones son X, X + N 1 , X + N 2 y X + N 1 + N 2 donde X es una solución para la configuración inicial dada. [6] Robert Eisele publicó una introducción a este método. [7]
El método de "persecución de luz" es similar a la eliminación gaussiana , que siempre resuelve el problema (si existe una solución), aunque con la posibilidad de muchos pasos redundantes. [2] [6] [8] En este enfoque, las filas se manipulan una a la vez, comenzando por la fila superior. Todas las luces se desactivan en la fila alternando las luces adyacentes en la fila directamente inferior. Luego, se utiliza el mismo método en las filas consecutivas hasta la última. La última fila se resuelve por separado, según sus luces activas. Las luces correspondientes (ver la tabla a continuación) en la fila superior se alternan y se ejecuta nuevamente el algoritmo inicial, lo que da como resultado una solución. [8]
Las tablas y estrategias para otros tamaños de tablero se generan jugando Lights Out con un tablero en blanco y observando el resultado de llevar una luz particular desde la fila superior a la fila inferior.
Una vez que se encuentra una única solución, se puede determinar una solución con el número mínimo de movimientos mediante la eliminación de conjuntos redundantes de pulsaciones de botones que no tienen efecto acumulativo. [6] [8]
Se ha demostrado la existencia de soluciones para una amplia variedad de configuraciones de tableros, como la hexagonal, [9] mientras que se han construido explícitamente soluciones para tableros n por n para n≤200. [10]
Existe una solución para cada caso N×N. Es solucionable en cualquier grafo no dirigido, donde al hacer clic en un vértice se invierte su valor y el de sus vecinos. En términos más generales, si la matriz de acción es simétrica, su diagonal siempre es solucionable. [11]