En matemáticas, el teorema de Newton sobre los óvalos establece que el área cortada por una secante de un óvalo convexo suave no es una función algebraica de la secante.
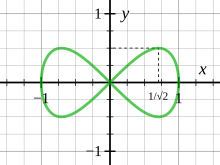
Isaac Newton lo enunció como lema 28 de la sección VI del libro 1 de los Principia de Newton , y lo utilizó para demostrar que la posición de un planeta que se mueve en una órbita no es una función algebraica del tiempo. Ha habido cierta controversia sobre si este teorema es correcto o no porque Newton no dijo exactamente qué quería decir con un óvalo, y para algunas interpretaciones de la palabra óvalo el teorema es correcto, mientras que para otras es falso. Si "óvalo" significa simplemente una curva convexa cerrada continua , entonces hay contraejemplos, como triángulos o uno de los lóbulos de la lemniscata de Huygens y 2 = x 2 − x 4 , mientras que Arnold (1989) señaló que si "óvalo" es una curva convexa infinitamente diferenciable , entonces la afirmación de Newton es correcta y su argumento tiene los pasos esenciales de una prueba rigurosa.
Vassiliev (2002) generalizó el teorema de Newton a dimensiones superiores.
La traducción al inglés de la declaración original de Newton (Newton 1962, lema 28 sección 6 libro I) es:
En lenguaje matemático moderno, Newton demostró esencialmente el siguiente teorema:
En otras palabras, "ovalado" en el enunciado de Newton debería significar "curva suave y convexa". La diferenciabilidad infinita en todos los puntos es necesaria: para cualquier entero positivo n hay curvas algebraicas que son suaves en todos los puntos excepto en uno y diferenciables n veces en el punto restante para el cual el área cortada por una secante es algebraica.
Newton observó que un argumento similar muestra que la longitud del arco de un óvalo (suave y convexo) entre dos puntos no está dada por una función algebraica de los puntos.

Newton tomó el origen P dentro del óvalo y consideró la espiral de puntos ( r , θ ) en coordenadas polares cuya distancia r desde P es el área cortada por las líneas desde P con ángulos 0 y θ . Luego observó que esta espiral no puede ser algebraica ya que tiene un número infinito de intersecciones con una línea que pasa por P , por lo que el área cortada por una secante no puede ser una función algebraica de la secante.
Esta prueba requiere que el óvalo y, por lo tanto, la espiral sean suaves; de lo contrario, la espiral podría ser una unión infinita de fragmentos de diferentes curvas algebraicas. Esto es lo que sucede en los diversos "contraejemplos" del teorema de Newton para óvalos no suaves.