
En matemáticas combinatorias , una secuencia de De Bruijn de orden n en un alfabeto A de tamaño k es una secuencia cíclica en la que cada posible cadena de longitud n en A ocurre exactamente una vez como subcadena (es decir, como una subsecuencia contigua ). Tal secuencia se denota por B ( k , n ) y tiene longitud k n , que también es el número de cadenas distintas de longitud n en A . Cada una de estas cadenas distintas, cuando se toma como una subcadena de B ( k , n ) , debe comenzar en una posición diferente, porque las subcadenas que comienzan en la misma posición no son distintas. Por lo tanto, B ( k , n ) debe tener al menos k n símbolos. Y dado que B ( k , n ) tiene exactamente k n símbolos, las secuencias de De Bruijn son óptimamente cortas con respecto a la propiedad de contener cada cadena de longitud n al menos una vez.
El número de secuencias distintas de De Bruijn B ( k , n ) es
Las secuencias reciben su nombre del matemático holandés Nicolaas Govert de Bruijn , quien escribió sobre ellas en 1946. [1] Como escribió más tarde, [2] la existencia de secuencias de De Bruijn para cada orden junto con las propiedades anteriores fueron demostradas por primera vez , para el caso de alfabetos con dos elementos, por Camille Flye Sainte-Marie (1894). La generalización a alfabetos más grandes se debe a Tatyana van Aardenne-Ehrenfest y De Bruijn (1951). Los autómatas para reconocer estas secuencias se denominan autómatas de Bruijn.
En la mayoría de las aplicaciones, A = {0,1}.
El ejemplo más antiguo conocido de una secuencia de Bruijn proviene de la prosodia sánscrita donde, desde el trabajo de Pingala , a cada posible patrón de tres sílabas de sílabas largas y cortas se le da un nombre, como 'y' para corto-largo-largo y 'm' para largo-largo-largo. Para recordar estos nombres, se utiliza la regla mnemotécnica yamātārājabhānasalagām , en la que cada patrón de tres sílabas aparece comenzando por su nombre: 'yamātā' tiene un patrón corto-largo-largo, 'mātārā' tiene un patrón largo-largo-largo, y así sucesivamente, hasta 'salagām' que tiene un patrón corto-corto-largo. Esta mnemotecnia, equivalente a una secuencia de Bruijn sobre 3-tuplas binarias, es de antigüedad desconocida, pero es al menos tan antigua como el libro de Charles Philip Brown de 1869 sobre prosodia sánscrita que la menciona y la considera "una línea antigua, escrita por Pāṇini ". [3]
En 1894, A. de Rivière planteó la cuestión en un número de la revista francesa de problemas L'Intermédiaire des Mathématiciens , de la existencia de una disposición circular de ceros y unos de tamaño que contenga todas las secuencias binarias de longitud . El problema fue resuelto (de manera afirmativa), junto con el recuento de soluciones distintas, por Camille Flye Sainte-Marie en el mismo año. [2] Esto fue en gran parte olvidado, y Martin (1934) demostró la existencia de tales ciclos para el tamaño general del alfabeto en lugar de 2, con un algoritmo para construirlos. Finalmente, cuando en 1944 Kees Posthumus conjeturó el recuento para secuencias binarias, de Bruijn demostró la conjetura en 1946, a través de la cual el problema se hizo conocido. [2]
Karl Popper describe estos objetos de forma independiente en su obra La lógica del descubrimiento científico (1934), llamándolos "secuencias aleatorias más cortas". [4]

Las secuencias de De Bruijn se pueden construir tomando un camino hamiltoniano de un gráfico de De Bruijn de n dimensiones sobre k símbolos (o equivalentemente, un ciclo euleriano de un gráfico de De Bruijn de ( n − 1) dimensiones). [5]
Una construcción alternativa implica concatenar juntas, en orden lexicográfico, todas las palabras de Lyndon cuya longitud divide a n . [6]
Se puede utilizar una transformada inversa de Burrows-Wheeler para generar las palabras Lyndon requeridas en orden lexicográfico. [7]
Las secuencias de Bruijn también se pueden construir utilizando registros de desplazamiento [8] o mediante campos finitos . [9]

Objetivo: construir una secuencia B (2, 4) de Bruijn de longitud 2 4 = 16 usando el ciclo del gráfico de Bruijn tridimensional euleriano ( n − 1 = 4 − 1 = 3).
Cada arista de este grafo tridimensional de De Bruijn corresponde a una secuencia de cuatro dígitos: los tres dígitos que etiquetan el vértice que la arista abandona seguidos por el que etiqueta la arista. Si se recorre la arista etiquetada 1 desde 000, se llega a 001, lo que indica la presencia de la subsecuencia 0001 en la secuencia de De Bruijn. Recorrer cada arista exactamente una vez es utilizar cada una de las 16 secuencias de cuatro dígitos exactamente una vez.
Por ejemplo, supongamos que seguimos el siguiente camino euleriano a través de estos vértices:
Estas son las secuencias de salida de longitud k :
Esto corresponde a la siguiente secuencia de De Bruijn:
Los ocho vértices aparecen en la secuencia de la siguiente manera:
{0 0 0 0} 1 1 1 1 0 1 1 0 0 1 0 1 0 {0 0 0 1} 1 1 1 0 1 1 0 0 1 0 1 0 0 {0 0 1 1} 1 1 0 1 1 0 0 1 0 1 0 0 0 {0 1 1 1} 1 0 1 1 0 0 1 0 1 0 0 0 0 {1 1 1 1} 0 1 1 0 0 1 0 1 0 0 0 0 1 {1 1 1 0} 1 1 0 0 1 0 1 0 0 0 0 1 1 {1 1 0 1} 1 0 0 1 0 1 0 0 0 0 1 1 1 {1 0 1 1} 0 0 1 0 1 0 0 0 0 1 1 1 1 {0 1 1 0} 0 1 0 1 0 0 0 0 1 1 1 1 0 {1 1 0 0} 1 0 1 0 0 0 0 1 1 1 1 0 1 {1 0 0 1} 0 1 0 0 0 0 1 1 1 1 0 1 1 {0 0 1 0} 1 0 0 0 0 1 1 1 1 0 1 1 0 {0 1 0 1} 0} 0 0 0 1 1 1 1 0 1 1 0 0 {1 0 1 ... ... 0 0} 0 0 1 1 1 1 0 1 1 0 0 1 {0 1 ... ... 0 0 0} 0 1 1 1 1 0 1 1 0 0 1 0 {1 ......y luego volvemos al punto de partida. Cada una de las ocho secuencias de 3 dígitos (que corresponden a los ocho vértices) aparece exactamente dos veces, y cada una de las dieciséis secuencias de 4 dígitos (que corresponden a las 16 aristas) aparece exactamente una vez.
Matemáticamente, una transformada inversa de Burrows-Wheeler sobre una palabra w genera un conjunto múltiple de clases de equivalencia que consisten en cadenas y sus rotaciones. [7] Cada una de estas clases de equivalencia de cadenas contiene una palabra Lyndon como elemento mínimo único, por lo que se puede considerar que la transformada inversa de Burrows-Wheeler genera un conjunto de palabras Lyndon. Se puede demostrar que si realizamos la transformada inversa de Burrows-Wheeler sobre una palabra w que consiste en el alfabeto de tamaño k repetido k n −1 veces (de modo que produzca una palabra de la misma longitud que la secuencia de De Bruijn deseada), entonces el resultado será el conjunto de todas las palabras Lyndon cuya longitud divida a n . De ello se deduce que ordenar estas palabras Lyndon en orden lexicográfico producirá una secuencia de De Bruijn B ( k , n ), y que esta será la primera secuencia de De Bruijn en orden lexicográfico. Se puede utilizar el siguiente método para realizar la transformada inversa de Burrows-Wheeler, utilizando su permutación estándar :
Por ejemplo, para construir la secuencia de Bruijn B (2,4) más pequeña de longitud 2 4 = 16, repita el alfabeto (ab) 8 veces y obtendrá w = abababababababab . Ordene los caracteres en w y obtendrá w ′ = aaaaaaaabbbbbbbb . Coloque w ′ sobre w como se muestra y asigne cada elemento en w ′ al elemento correspondiente en w dibujando una línea. Numere las columnas como se muestra para que podamos leer los ciclos de la permutación:
Comenzando desde la izquierda, los ciclos de notación de permutación estándar son: (1) (2 3 5 9) (4 7 13 10) (6 11) (8 15 14 12) (16) . (Permutación estándar)
Luego, reemplazando cada número por la letra correspondiente en w ′ de esa columna se obtiene: (a)(aaab)(aabb)(ab)(abbb)(b) .
Estas son todas las palabras de Lyndon cuya longitud divide a 4, en orden lexicográfico, por lo que al eliminar los paréntesis se obtiene B (2,4) = aaaabaabbababbbb .
El siguiente código Python calcula una secuencia de Bruijn, dados k y n , basándose en un algoritmo de Generación Combinatoria de Frank Ruskey . [10]
de escribir import Iterable , Any def de_bruijn ( k : Iterable [ str ] | int , n : int ) -> str : """Secuencia de Bruijn para el alfabeto k y subsecuencias de longitud n. """ # Dos tipos de entrada de alfabeto: un entero se expande # a una lista de enteros como el alfabeto.. if isinstance ( k , int ): alphabet = list ( map ( str , range ( k ))) else : # Mientras que cualquier tipo de lista se utiliza tal como está alphabet = k k = len ( k ) a = [ 0 ] * k * n secuencia = [] def db ( t , p ): si t > n : si n % p == 0 : secuencia . extend ( a [ 1 : p + 1 ]) de lo contrario : a [ t ] = a [ t - p ] db ( t + 1 , p ) para j en rango ( a [ t - p ] + 1 , k ): a [ t ] = j db ( t + 1 , t ) db ( 1,1 ) devuelve " " .join ( alfabeto [ i ] para i en secuencia ) imprimir ( de_bruijn ( 2 , 3 )) imprimir ( de_bruijn ( "abcd" , 2 ))que impresiones
00010111aabacadbbcbdccdd
Tenga en cuenta que se entiende que estas secuencias se "enrollan" en un ciclo. Por ejemplo, la primera secuencia contiene 110 y 100 de esta manera.
Los ciclos de De Bruijn son de uso general en experimentos de neurociencia y psicología que examinan el efecto del orden de los estímulos sobre los sistemas neuronales, [11] y pueden diseñarse especialmente para su uso con imágenes por resonancia magnética funcional . [12]
Los símbolos de una secuencia de De Bruijn escrita alrededor de un objeto circular (como la rueda de un robot ) se pueden utilizar para identificar su ángulo examinando los n símbolos consecutivos que miran hacia un punto fijo. Este problema de codificación de ángulos se conoce como el "problema del tambor giratorio". [13] Los códigos Gray se pueden utilizar como mecanismos de codificación posicional rotatorio similares, un método que se encuentra comúnmente en los codificadores rotatorios .
Se puede utilizar una secuencia de De Bruijn para encontrar rápidamente el índice del bit menos significativo del conjunto ("1 más a la derecha") o el bit más significativo del conjunto ("1 más a la izquierda") en una palabra mediante operaciones bit a bit y multiplicación. [14] El siguiente ejemplo utiliza una secuencia de De Bruijn para determinar el índice del bit menos significativo del conjunto (equivalente a contar la cantidad de bits '0' finales) en un entero sin signo de 32 bits:
uint8_t lowestBitIndex ( uint32_t v ) { static const uint8_t BitPositionLookup [ 32 ] = // tabla hash { 0 , 1 , 28 , 2 , 29 , 14 , 24 , 3 , 30 , 22 , 20 , 15 , 25 , 17 , 4 , 8 , 31 , 27 , 13 , 23 , 21 , 19 , 16 , 7 , 26 , 12 , 18 , 6 , 11 , 5 , 10 , 9 }; devolver BitPositionLookup [(( uint32_t )(( v & - v ) * 0x077CB531U )) >> 27 ]; } La lowestBitIndex()función devuelve el índice del bit menos significativo establecido en v , o cero si v no tiene bits establecidos. La constante 0x077CB531U en la expresión es la secuencia B (2, 5) 0000 0111 0111 1100 1011 0101 0011 0001 (se agregaron espacios para mayor claridad). La operación (v & -v)pone a cero todos los bits excepto el bit menos significativo establecido, lo que da como resultado un nuevo valor que es una potencia de 2. Esta potencia de 2 se multiplica (módulo aritmético 2 32 ) por la secuencia de De Bruijn, lo que produce un producto de 32 bits en el que la secuencia de bits de los 5 MSB es única para cada potencia de 2. Los 5 MSB se desplazan a las posiciones LSB para producir un código hash en el rango [0, 31], que luego se usa como índice en la tabla hash BitPositionLookup. El valor de la tabla hash seleccionada es el índice de bit del bit establecido menos significativo en v .
El siguiente ejemplo determina el índice del bit más significativo establecido en un entero sin signo de 32 bits:
uint32_t keepHighestBit ( uint32_t n ) { n |= ( n >> 1 ); n |= ( n >> 2 ) ; n |= ( n >> 4 ); n |= ( n >> 8 ); n |= ( n >> 16 ); devolver n - ( n >> 1 ); } uint8_t lowestBitIndex ( uint32_t v ) { static const uint8_t BitPositionLookup [ 32 ] = { // tabla hash 0 , 1 , 16 , 2 , 29 , 17 , 3 , 22 , 30 , 20 , 18 , 11 , 13 , 4 , 7 , 23 , 31 , 15 , 28 , 21 , 19 , 10 , 12 , 6 , 14 , 27 , 9 , 5 , 26 , 8 , 25 , 24 , }; devolver BitPositionLookup [( keepHighestBit ( v ) * 0x06EB14F9U ) >> 27 ]; } En el ejemplo anterior se utiliza una secuencia de Bruijn alternativa (0x06EB14F9U), con la reordenación correspondiente de los valores de la matriz. La elección de esta secuencia de Bruijn en particular es arbitraria, pero los valores de la tabla hash deben ordenarse para que coincidan con la secuencia de Bruijn elegida. La keepHighestBit()función pone a cero todos los bits excepto el bit del conjunto más significativo, lo que da como resultado un valor que es una potencia de 2, que luego se procesa como en el ejemplo anterior.

Se puede utilizar una secuencia de De Bruijn para acortar un ataque de fuerza bruta en una cerradura con código tipo PIN que no tiene una tecla "enter" y acepta los últimos n dígitos ingresados. Por ejemplo, una cerradura de puerta digital con un código de 4 dígitos (cada dígito con 10 posibilidades, de 0 a 9) tendría B (10, 4) soluciones, con una longitud10 000 . Por lo tanto, sólo como máximo10 000 + 3 =Se necesitan 10 003 (ya que las soluciones son cíclicas) pulsaciones para abrir la cerradura, mientras que probar todos los códigos por separado requeriría 4 ×10 000 =40.000 prensas .
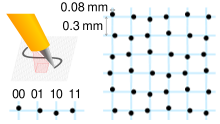
Una secuencia de Bruijn n-aria f-fold es una extensión de la noción de secuencia de Bruijn n -aria, de modo que la secuencia de longitud contiene cada subsecuencia posible de longitud n exactamente f veces. Por ejemplo, para las secuencias cíclicas 11100010 y 11101000 son secuencias de Bruijn binarias dobles. El número de secuencias de Bruijn dobles, para es , los otros números conocidos [16] son , , y .
Un toro de Bruijn es una matriz toroidal con la propiedad de que cada matriz k - aria m -por- n ocurre exactamente una vez.
Este patrón se puede utilizar para la codificación posicional bidimensional de una manera análoga a la descrita anteriormente para la codificación rotatoria. La posición se puede determinar examinando la matriz m por n directamente adyacente al sensor y calculando su posición en el toro de Bruijn.
El cálculo de la posición de una tupla o matriz única particular en una secuencia o toro de De Bruijn se conoce como el problema de decodificación de De Bruijn . Existen algoritmos de decodificación eficientes para secuencias especiales construidas recursivamente [17] y se extienden al caso bidimensional. [18] La decodificación de De Bruijn es de interés, por ejemplo, en casos en los que se utilizan secuencias o toros grandes para la codificación posicional.
{{cite journal}}: Mantenimiento de CS1: postscript ( enlace )