Las derivadas de escalares , vectores y tensores de segundo orden con respecto a tensores de segundo orden son de considerable utilidad en mecánica de medios continuos . Estas derivadas se utilizan en las teorías de elasticidad y plasticidad no lineales , particularmente en el diseño de algoritmos para simulaciones numéricas . [1]
La derivada direccional proporciona una forma sistemática de encontrar estas derivadas. [2]
Derivadas respecto de vectores y tensores de segundo orden A continuación se ofrecen las definiciones de derivadas direccionales para diversas situaciones. Se supone que las funciones son lo suficientemente suaves como para que se puedan obtener derivadas.
Derivadas de funciones escalares de vectores Sea f ( v ) una función de valor real del vector v . Entonces la derivada de f ( v ) con respecto a v (o en v ) es el vector definido a través de su producto escalar con cualquier vector u siendo
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
para todos los vectores u . El producto escalar anterior produce un escalar, y si u es un vector unitario da la derivada direccional de f en v , en la dirección u .
Propiedades:
Si entonces f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )+f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}+{\frac {\partial f_{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} } Si entonces f ( v ) = f 1 ( v ) f 2 ( v ) {\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )~f_{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) f 2 ( v ) + f 1 ( v ) ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v} )+f_{1}(\mathbf {v} )~\left({\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} Si entonces f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle f(\mathbf {v} )=f_{1}(f_{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ∂ f 2 ∂ v ⋅ u {\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~{\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} }
Derivadas de funciones vectoriales con valores vectoriales Sea f ( v ) una función vectorial del vector v . Entonces la derivada de f ( v ) con respecto a v (o en v ) es el tensor de segundo orden definido a través de su producto escalar con cualquier vector u siendo
∂ f ∂ v ⋅ u = D f ( v ) [ u ] = [ d d α f ( v + α u ) ] α = 0 {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
para todos los vectores u . El producto escalar anterior produce un vector, y si u es un vector unitario da la derivada direccional de f en v , en la dirección u .
Propiedades:
Si entonces f ( v ) = f 1 ( v ) + f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )+\mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v + ∂ f 2 ∂ v ) ⋅ u {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}+{\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} } Si entonces f ( v ) = f 1 ( v ) × f 2 ( v ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )\times \mathbf {f} _{2}(\mathbf {v} )} ∂ f ∂ v ⋅ u = ( ∂ f 1 ∂ v ⋅ u ) × f 2 ( v ) + f 1 ( v ) × ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)\times \mathbf {f} _{2}(\mathbf {v} )+\mathbf {f} _{1}(\mathbf {v} )\times \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)} Si entonces f ( v ) = f 1 ( f 2 ( v ) ) {\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {f} _{2}(\mathbf {v} ))} ∂ f ∂ v ⋅ u = ∂ f 1 ∂ f 2 ⋅ ( ∂ f 2 ∂ v ⋅ u ) {\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {f} _{2}}}\cdot \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)}
Derivadas de funciones escalares de tensores de segundo orden Sea una función de valor real del tensor de segundo orden . Entonces la derivada de con respecto a (o en ) en la dirección es el tensor de segundo orden definido como
para todos los tensores de segundo orden . f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} f ( S ) {\displaystyle f({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} S {\displaystyle {\boldsymbol {S}}} T {\displaystyle {\boldsymbol {T}}} ∂ f ∂ S : T = D f ( S ) [ T ] = [ d d α f ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} T {\displaystyle {\boldsymbol {T}}}
Propiedades:
Si entonces f ( S ) = f 1 ( S ) + f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})+f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S + ∂ f 2 ∂ S ) : T {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}} Si entonces f ( S ) = f 1 ( S ) f 2 ( S ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})~f_{2}({\boldsymbol {S}})} ∂ f ∂ S : T = ( ∂ f 1 ∂ S : T ) f 2 ( S ) + f 1 ( S ) ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)~f_{2}({\boldsymbol {S}})+f_{1}({\boldsymbol {S}})~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Si entonces f ( S ) = f 1 ( f 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}(f_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ f 2 ( ∂ f 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial f_{2}}}~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
Derivadas de funciones tensoriales de tensores de segundo orden Sea una función tensorial de segundo orden del tensor de segundo orden . Entonces la derivada de con respecto a (o en ) en la dirección es el tensor de cuarto orden definido como
para todos los tensores de segundo orden . F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} F ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})} S {\displaystyle {\boldsymbol {S}}} S {\displaystyle {\boldsymbol {S}}} T {\displaystyle {\boldsymbol {T}}} ∂ F ∂ S : T = D F ( S ) [ T ] = [ d d α F ( S + α T ) ] α = 0 {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}} T {\displaystyle {\boldsymbol {T}}}
Propiedades:
Si entonces F ( S ) = F 1 ( S ) + F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})+{\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S + ∂ F 2 ∂ S ) : T {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}} Si entonces F ( S ) = F 1 ( S ) ⋅ F 2 ( S ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})} ∂ F ∂ S : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 ( S ) + F 1 ( S ) ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})+{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Si entonces F ( S ) = F 1 ( F 2 ( S ) ) {\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ F ∂ S : T = ∂ F 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)} Si entonces f ( S ) = f 1 ( F 2 ( S ) ) {\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))} ∂ f ∂ S : T = ∂ f 1 ∂ F 2 : ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
Gradiente de un campo tensorial El gradiente , , de un campo tensorial en la dirección de un vector constante arbitrario c se define como:
El gradiente de un campo tensorial de orden n es un campo tensorial de orden n +1. ∇ T {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}} T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} ∇ T ⋅ c = lim α → 0 d d α T ( x + α c ) {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} =\lim _{\alpha \rightarrow 0}\quad {\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(\mathbf {x} +\alpha \mathbf {c} )}
Coordenadas cartesianas Si son los vectores base en un sistema de coordenadas cartesianas , con coordenadas de puntos denotadas por ( ), entonces el gradiente del campo tensorial está dado por e 1 , e 2 , e 3 {\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}} x 1 , x 2 , x 3 {\displaystyle x_{1},x_{2},x_{3}} T {\displaystyle {\boldsymbol {T}}} ∇ T = ∂ T ∂ x i ⊗ e i {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i}}
Como los vectores base no varían en un sistema de coordenadas cartesianas, tenemos las siguientes relaciones para los gradientes de un campo escalar , un campo vectorial v y un campo tensorial de segundo orden . ϕ {\displaystyle \phi } S {\displaystyle {\boldsymbol {S}}} ∇ ϕ = ∂ ϕ ∂ x i e i = ϕ , i e i ∇ v = ∂ ( v j e j ) ∂ x i ⊗ e i = ∂ v j ∂ x i e j ⊗ e i = v j , i e j ⊗ e i ∇ S = ∂ ( S j k e j ⊗ e k ) ∂ x i ⊗ e i = ∂ S j k ∂ x i e j ⊗ e k ⊗ e i = S j k , i e j ⊗ e k ⊗ e i {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\cfrac {\partial \phi }{\partial x_{i}}}~\mathbf {e} _{i}=\phi _{,i}~\mathbf {e} _{i}\\{\boldsymbol {\nabla }}\mathbf {v} &={\cfrac {\partial (v_{j}\mathbf {e} _{j})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial v_{j}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}=v_{j,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\cfrac {\partial (S_{jk}\mathbf {e} _{j}\otimes \mathbf {e} _{k})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial S_{jk}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}=S_{jk,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}\end{aligned}}}
Coordenadas curvilíneas Si son los vectores base contravariantes en un sistema de coordenadas curvilíneas , con coordenadas de puntos denotadas por ( ), entonces el gradiente del campo tensorial está dado por (ver [3] para una prueba). g 1 , g 2 , g 3 {\displaystyle \mathbf {g} ^{1},\mathbf {g} ^{2},\mathbf {g} ^{3}} ξ 1 , ξ 2 , ξ 3 {\displaystyle \xi ^{1},\xi ^{2},\xi ^{3}} T {\displaystyle {\boldsymbol {T}}} ∇ T = ∂ T ∂ ξ i ⊗ g i {\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\frac {\partial {\boldsymbol {T}}}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}}
De esta definición tenemos las siguientes relaciones para los gradientes de un campo escalar , un campo vectorial v y un campo tensorial de segundo orden . ϕ {\displaystyle \phi } S {\displaystyle {\boldsymbol {S}}} ∇ ϕ = ∂ ϕ ∂ ξ i g i ∇ v = ∂ ( v j g j ) ∂ ξ i ⊗ g i = ( ∂ v j ∂ ξ i + v k Γ i k j ) g j ⊗ g i = ( ∂ v j ∂ ξ i − v k Γ i j k ) g j ⊗ g i ∇ S = ∂ ( S j k g j ⊗ g k ) ∂ ξ i ⊗ g i = ( ∂ S j k ∂ ξ i − S l k Γ i j l − S j l Γ i k l ) g j ⊗ g k ⊗ g i {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\frac {\partial \phi }{\partial \xi ^{i}}}~\mathbf {g} ^{i}\\{\boldsymbol {\nabla }}\mathbf {v} &={\frac {\partial \left(v^{j}\mathbf {g} _{j}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}=\left({\frac {\partial v^{j}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{j}\right)~\mathbf {g} _{j}\otimes \mathbf {g} ^{i}=\left({\frac {\partial v_{j}}{\partial \xi ^{i}}}-v_{k}~\Gamma _{ij}^{k}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\frac {\partial \left(S_{jk}~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}=\left({\frac {\partial S_{jk}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ij}^{l}-S_{jl}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\otimes \mathbf {g} ^{i}\end{aligned}}}
donde el símbolo de Christoffel se define utilizando Γ i j k {\displaystyle \Gamma _{ij}^{k}} Γ i j k g k = ∂ g i ∂ ξ j ⟹ Γ i j k = ∂ g i ∂ ξ j ⋅ g k = − g i ⋅ ∂ g k ∂ ξ j {\displaystyle \Gamma _{ij}^{k}~\mathbf {g} _{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\quad \implies \quad \Gamma _{ij}^{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\cdot \mathbf {g} ^{k}=-\mathbf {g} _{i}\cdot {\frac {\partial \mathbf {g} ^{k}}{\partial \xi ^{j}}}}
Coordenadas polares cilíndricas En coordenadas cilíndricas , el gradiente viene dado por ∇ ϕ = ∂ ϕ ∂ r e r + 1 r ∂ ϕ ∂ θ e θ + ∂ ϕ ∂ z e z ∇ v = ∂ v r ∂ r e r ⊗ e r + 1 r ( ∂ v r ∂ θ − v θ ) e r ⊗ e θ + ∂ v r ∂ z e r ⊗ e z + ∂ v θ ∂ r e θ ⊗ e r + 1 r ( ∂ v θ ∂ θ + v r ) e θ ⊗ e θ + ∂ v θ ∂ z e θ ⊗ e z + ∂ v z ∂ r e z ⊗ e r + 1 r ∂ v z ∂ θ e z ⊗ e θ + ∂ v z ∂ z e z ⊗ e z ∇ S = ∂ S r r ∂ r e r ⊗ e r ⊗ e r + ∂ S r r ∂ z e r ⊗ e r ⊗ e z + 1 r [ ∂ S r r ∂ θ − ( S θ r + S r θ ) ] e r ⊗ e r ⊗ e θ + ∂ S r θ ∂ r e r ⊗ e θ ⊗ e r + ∂ S r θ ∂ z e r ⊗ e θ ⊗ e z + 1 r [ ∂ S r θ ∂ θ + ( S r r − S θ θ ) ] e r ⊗ e θ ⊗ e θ + ∂ S r z ∂ r e r ⊗ e z ⊗ e r + ∂ S r z ∂ z e r ⊗ e z ⊗ e z + 1 r [ ∂ S r z ∂ θ − S θ z ] e r ⊗ e z ⊗ e θ + ∂ S θ r ∂ r e θ ⊗ e r ⊗ e r + ∂ S θ r ∂ z e θ ⊗ e r ⊗ e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e θ ⊗ e r ⊗ e θ + ∂ S θ θ ∂ r e θ ⊗ e θ ⊗ e r + ∂ S θ θ ∂ z e θ ⊗ e θ ⊗ e z + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ ⊗ e θ ⊗ e θ + ∂ S θ z ∂ r e θ ⊗ e z ⊗ e r + ∂ S θ z ∂ z e θ ⊗ e z ⊗ e z + 1 r [ ∂ S θ z ∂ θ + S r z ] e θ ⊗ e z ⊗ e θ + ∂ S z r ∂ r e z ⊗ e r ⊗ e r + ∂ S z r ∂ z e z ⊗ e r ⊗ e z + 1 r [ ∂ S z r ∂ θ − S z θ ] e z ⊗ e r ⊗ e θ + ∂ S z θ ∂ r e z ⊗ e θ ⊗ e r + ∂ S z θ ∂ z e z ⊗ e θ ⊗ e z + 1 r [ ∂ S z θ ∂ θ + S z r ] e z ⊗ e θ ⊗ e θ + ∂ S z z ∂ r e z ⊗ e z ⊗ e r + ∂ S z z ∂ z e z ⊗ e z ⊗ e z + 1 r ∂ S z z ∂ θ e z ⊗ e z ⊗ e θ {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad &{\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}
Divergencia de un campo tensorial La divergencia de un campo tensorial se define utilizando la relación recursiva T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} ( ∇ ⋅ T ) ⋅ c = ∇ ⋅ ( c ⋅ T T ) ; ∇ ⋅ v = tr ( ∇ v ) {\displaystyle ({\boldsymbol {\nabla }}\cdot {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot \left(\mathbf {c} \cdot {\boldsymbol {T}}^{\textsf {T}}\right)~;\qquad {\boldsymbol {\nabla }}\cdot \mathbf {v} ={\text{tr}}({\boldsymbol {\nabla }}\mathbf {v} )}
donde c es un vector constante arbitrario y v es un campo vectorial. Si es un campo tensorial de orden n > 1 entonces la divergencia del campo es un tensor de orden n − 1. T {\displaystyle {\boldsymbol {T}}}
Coordenadas cartesianas En un sistema de coordenadas cartesianas tenemos las siguientes relaciones para un campo vectorial v y un campo tensorial de segundo orden . S {\displaystyle {\boldsymbol {S}}} ∇ ⋅ v = ∂ v i ∂ x i = v i , i ∇ ⋅ S = ∂ S i k ∂ x i e k = S i k , i e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &={\frac {\partial v_{i}}{\partial x_{i}}}=v_{i,i}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\frac {\partial S_{ik}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ik,i}~\mathbf {e} _{k}\end{aligned}}}
donde la notación de índice tensorial para derivadas parciales se utiliza en las expresiones más a la derecha. Nótese que ∇ ⋅ S ≠ ∇ ⋅ S T . {\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}\neq {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}^{\textsf {T}}.}
Para un tensor simétrico de segundo orden, la divergencia también suele escribirse como [4]
∇ ⋅ S = ∂ S k i ∂ x i e k = S k i , i e k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\cfrac {\partial S_{ki}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ki,i}~\mathbf {e} _{k}\end{aligned}}}
La expresión anterior se utiliza a veces como definición de en forma de componente cartesiano (a menudo también se escribe como ). Tenga en cuenta que dicha definición no es coherente con el resto de este artículo (consulte la sección sobre coordenadas curvilíneas). ∇ ⋅ S {\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}} div S {\displaystyle \operatorname {div} {\boldsymbol {S}}}
La diferencia radica en si la diferenciación se realiza con respecto a las filas o columnas de , y es convencional. Esto se demuestra con un ejemplo. En un sistema de coordenadas cartesianas, el tensor (matriz) de segundo orden es el gradiente de una función vectorial . S {\displaystyle {\boldsymbol {S}}} S {\displaystyle \mathbf {S} } v {\displaystyle \mathbf {v} }
∇ ⋅ ( ∇ v ) = ∇ ⋅ ( v i , j e i ⊗ e j ) = v i , j i e i ⋅ e i ⊗ e j = ( ∇ ⋅ v ) , j e j = ∇ ( ∇ ⋅ v ) ∇ ⋅ [ ( ∇ v ) T ] = ∇ ⋅ ( v j , i e i ⊗ e j ) = v j , i i e i ⋅ e i ⊗ e j = ∇ 2 v j e j = ∇ 2 v {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
La última ecuación es equivalente a la definición/interpretación alternativa [4]
( ∇ ⋅ ) alt ( ∇ v ) = ( ∇ ⋅ ) alt ( v i , j e i ⊗ e j ) = v i , j j e i ⊗ e j ⋅ e j = ∇ 2 v i e i = ∇ 2 v {\displaystyle {\begin{aligned}\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left({\boldsymbol {\nabla }}\mathbf {v} \right)=\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,jj}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\cdot \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{i}~\mathbf {e} _{i}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
Coordenadas curvilíneas En coordenadas curvilíneas, las divergencias de un campo vectorial v y un campo tensorial de segundo orden son S {\displaystyle {\boldsymbol {S}}} ∇ ⋅ v = ( ∂ v i ∂ ξ i + v k Γ i k i ) ∇ ⋅ S = ( ∂ S i k ∂ ξ i − S l k Γ i i l − S i l Γ i k l ) g k {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &=\left({\cfrac {\partial v^{i}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{i}\right)\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left({\cfrac {\partial S_{ik}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ii}^{l}-S_{il}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{k}\end{aligned}}}
De manera más general, ∇ ⋅ S = [ ∂ S i j ∂ q k − Γ k i l S l j − Γ k j l S i l ] g i k b j = [ ∂ S i j ∂ q i + Γ i l i S l j + Γ i l j S i l ] b j = [ ∂ S j i ∂ q i + Γ i l i S j l − Γ i j l S l i ] b j = [ ∂ S i j ∂ q k − Γ i k l S l j + Γ k l j S i l ] g i k b j {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~S^{lj}+\Gamma _{il}^{j}~S^{il}\right]~\mathbf {b} _{j}\\[8pt]&=\left[{\cfrac {\partial S_{~j}^{i}}{\partial q^{i}}}+\Gamma _{il}^{i}~S_{~j}^{l}-\Gamma _{ij}^{l}~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{\partial q^{k}}}-\Gamma _{ik}^{l}~S_{l}^{~j}+\Gamma _{kl}^{j}~S_{i}^{~l}\right]~g^{ik}~\mathbf {b} _{j}\end{aligned}}}
Coordenadas polares cilíndricas En coordenadas polares cilíndricas ∇ ⋅ v = ∂ v r ∂ r + 1 r ( ∂ v θ ∂ θ + v r ) + ∂ v z ∂ z ∇ ⋅ S = ∂ S r r ∂ r e r + ∂ S r θ ∂ r e θ + ∂ S r z ∂ r e z + 1 r [ ∂ S θ r ∂ θ + ( S r r − S θ θ ) ] e r + 1 r [ ∂ S θ θ ∂ θ + ( S r θ + S θ r ) ] e θ + 1 r [ ∂ S θ z ∂ θ + S r z ] e z + ∂ S z r ∂ z e r + ∂ S z θ ∂ z e θ + ∂ S z z ∂ z e z {\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}
Rizo de un campo tensorial El rizo de un campo tensorial de orden n > 1 también se define utilizando la relación recursiva
donde c es un vector constante arbitrario y v es un campo vectorial. T ( x ) {\displaystyle {\boldsymbol {T}}(\mathbf {x} )} ( ∇ × T ) ⋅ c = ∇ × ( c ⋅ T ) ; ( ∇ × v ) ⋅ c = ∇ ⋅ ( v × c ) {\displaystyle ({\boldsymbol {\nabla }}\times {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {T}})~;\qquad ({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )}
Rizo de un campo tensorial (vectorial) de primer orden Consideremos un campo vectorial v y un vector constante arbitrario c . En notación de índice, el producto vectorial se da por
donde es el símbolo de permutación , también conocido como el símbolo de Levi-Civita. Entonces,
Por lo tanto, v × c = ε i j k v j c k e i {\displaystyle \mathbf {v} \times \mathbf {c} =\varepsilon _{ijk}~v_{j}~c_{k}~\mathbf {e} _{i}} ε i j k {\displaystyle \varepsilon _{ijk}} ∇ ⋅ ( v × c ) = ε i j k v j , i c k = ( ε i j k v j , i e k ) ⋅ c = ( ∇ × v ) ⋅ c {\displaystyle {\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )=\varepsilon _{ijk}~v_{j,i}~c_{k}=(\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} } ∇ × v = ε i j k v j , i e k {\displaystyle {\boldsymbol {\nabla }}\times \mathbf {v} =\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k}}
Rizo de un campo tensorial de segundo orden Para un tensor de segundo orden
Por lo tanto, utilizando la definición del rotacional de un campo tensorial de primer orden,
Por lo tanto, tenemos S {\displaystyle {\boldsymbol {S}}} c ⋅ S = c m S m j e j {\displaystyle \mathbf {c} \cdot {\boldsymbol {S}}=c_{m}~S_{mj}~\mathbf {e} _{j}} ∇ × ( c ⋅ S ) = ε i j k c m S m j , i e k = ( ε i j k S m j , i e k ⊗ e m ) ⋅ c = ( ∇ × S ) ⋅ c {\displaystyle {\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {S}})=\varepsilon _{ijk}~c_{m}~S_{mj,i}~\mathbf {e} _{k}=(\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times {\boldsymbol {S}})\cdot \mathbf {c} } ∇ × S = ε i j k S m j , i e k ⊗ e m {\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {S}}=\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m}}
Identidades que involucran el rotacional de un campo tensorial La identidad más comúnmente utilizada que involucra el rotacional de un cuerpo tensorial, , es
Esta identidad es válida para cuerpos tensoriales de todos los órdenes. Para el caso importante de un tensor de segundo orden, , esta identidad implica que T {\displaystyle {\boldsymbol {T}}} ∇ × ( ∇ T ) = 0 {\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {T}})={\boldsymbol {0}}} S {\displaystyle {\boldsymbol {S}}} ∇ × ( ∇ S ) = 0 ⟹ S m i , j − S m j , i = 0 {\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {S}})={\boldsymbol {0}}\quad \implies \quad S_{mi,j}-S_{mj,i}=0}
Derivada del determinante de un tensor de segundo orden La derivada del determinante de un tensor de segundo orden está dada por A {\displaystyle {\boldsymbol {A}}} ∂ ∂ A det ( A ) = det ( A ) [ A − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
En una base ortonormal, los componentes de se pueden escribir como una matriz A . En ese caso, el lado derecho corresponde a los cofactores de la matriz. A {\displaystyle {\boldsymbol {A}}}
Derivadas de los invariantes de un tensor de segundo orden Los invariantes principales de un tensor de segundo orden son I 1 ( A ) = tr A I 2 ( A ) = 1 2 [ ( tr A ) 2 − tr A 2 ] I 3 ( A ) = det ( A ) {\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A}})&={\frac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}
Las derivadas de estos tres invariantes con respecto a son A {\displaystyle {\boldsymbol {A}}} ∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = det ( A ) [ A − 1 ] T = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Prueba De la derivada del determinante sabemos que ∂ I 3 ∂ A = det ( A ) [ A − 1 ] T . {\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
Para las derivadas de los otros dos invariantes, volvamos a la ecuación característica det ( λ 1 + A ) = λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) . {\displaystyle \det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})~.}
Utilizando el mismo enfoque que para el determinante de un tensor, podemos demostrar que ∂ ∂ A det ( λ 1 + A ) = det ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T . {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}
Ahora el lado izquierdo se puede expandir como ∂ ∂ A det ( λ 1 + A ) = ∂ ∂ A [ λ 3 + I 1 ( A ) λ 2 + I 2 ( A ) λ + I 3 ( A ) ] = ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A . {\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}
Por lo tanto
o, ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A = det ( λ 1 + A ) [ ( λ 1 + A ) − 1 ] T {\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}} ( λ 1 + A ) T ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = det ( λ 1 + A ) 1 . {\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}
Al expandir el lado derecho y separar los términos del lado izquierdo se obtiene ( λ 1 + A T ) ⋅ [ ∂ I 1 ∂ A λ 2 + ∂ I 2 ∂ A λ + ∂ I 3 ∂ A ] = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 {\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}
o, [ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ ] 1 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
Si definimos y , podemos escribir lo anterior como I 0 := 1 {\displaystyle I_{0}:=1} I 4 := 0 {\displaystyle I_{4}:=0} [ ∂ I 1 ∂ A λ 3 + ∂ I 2 ∂ A λ 2 + ∂ I 3 ∂ A λ + ∂ I 4 ∂ A ] 1 + A T ⋅ ∂ I 0 ∂ A λ 3 + A T ⋅ ∂ I 1 ∂ A λ 2 + A T ⋅ ∂ I 2 ∂ A λ + A T ⋅ ∂ I 3 ∂ A = [ I 0 λ 3 + I 1 λ 2 + I 2 λ + I 3 ] 1 . {\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
Reuniendo términos que contienen varias potencias de λ, obtenemos λ 3 ( I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A ) + λ 2 ( I 1 1 − ∂ I 2 ∂ A 1 − A T ⋅ ∂ I 1 ∂ A ) + λ ( I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A ) + ( I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A ) = 0 . {\displaystyle {\begin{aligned}\lambda ^{3}&\left(I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}\right)+\lambda ^{2}\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}\right)+\\&\qquad \qquad \lambda \left(I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}\right)+\left(I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right)=0~.\end{aligned}}}
Entonces, invocando la arbitrariedad de λ, tenemos I 0 1 − ∂ I 1 ∂ A 1 − A T ⋅ ∂ I 0 ∂ A = 0 I 1 1 − ∂ I 2 ∂ A 1 − I 2 1 − ∂ I 3 ∂ A 1 − A T ⋅ ∂ I 2 ∂ A = 0 I 3 1 − ∂ I 4 ∂ A 1 − A T ⋅ ∂ I 3 ∂ A = 0 . {\displaystyle {\begin{aligned}I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}&=0\\I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=0\\I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=0~.\end{aligned}}}
Esto implica que ∂ I 1 ∂ A = 1 ∂ I 2 ∂ A = I 1 1 − A T ∂ I 3 ∂ A = I 2 1 − A T ( I 1 1 − A T ) = ( A 2 − I 1 A + I 2 1 ) T {\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Derivada del tensor identidad de segundo orden Sea el tensor identidad de segundo orden. Entonces la derivada de este tensor con respecto a un tensor de segundo orden está dada por
Esto se debe a que es independiente de . 1 {\displaystyle {\boldsymbol {\mathit {1}}}} A {\displaystyle {\boldsymbol {A}}} ∂ 1 ∂ A : T = 0 : T = 0 {\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {0}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}} 1 {\displaystyle {\boldsymbol {\mathit {1}}}} A {\displaystyle {\boldsymbol {A}}}
Derivada de un tensor de segundo orden con respecto a sí mismo Sea un tensor de segundo orden. Entonces A {\displaystyle {\boldsymbol {A}}} ∂ A ∂ A : T = [ ∂ ∂ α ( A + α T ) ] α = 0 = T = I : T {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}
Por lo tanto, ∂ A ∂ A = I {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}}
Aquí está el tensor identidad de cuarto orden. En notación de índice con respecto a una base ortonormal. I {\displaystyle {\boldsymbol {\mathsf {I}}}} I = δ i k δ j l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}=\delta _{ik}~\delta _{jl}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Este resultado implica que
donde ∂ A T ∂ A : T = I T : T = T T {\displaystyle {\frac {\partial {\boldsymbol {A}}^{\textsf {T}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}^{\textsf {T}}:{\boldsymbol {T}}={\boldsymbol {T}}^{\textsf {T}}} I T = δ j k δ i l e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{\textsf {T}}=\delta _{jk}~\delta _{il}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Por lo tanto, si el tensor es simétrico, entonces la derivada también es simétrica y obtenemos
donde el tensor identidad simétrico de cuarto orden es A {\displaystyle {\boldsymbol {A}}} ∂ A ∂ A = I ( s ) = 1 2 ( I + I T ) {\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~\left({\boldsymbol {\mathsf {I}}}+{\boldsymbol {\mathsf {I}}}^{\textsf {T}}\right)} I ( s ) = 1 2 ( δ i k δ j l + δ i l δ j k ) e i ⊗ e j ⊗ e k ⊗ e l {\displaystyle {\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~(\delta _{ik}~\delta _{jl}+\delta _{il}~\delta _{jk})~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Derivada de la inversa de un tensor de segundo orden Sean y dos tensores de segundo orden, entonces
En notación de índice con respecto a una base ortonormal
También tenemos
En notación de índice
Si el tensor es simétrico entonces A {\displaystyle {\boldsymbol {A}}} T {\displaystyle {\boldsymbol {T}}} ∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}} ∂ A i j − 1 ∂ A k l T k l = − A i k − 1 T k l A l j − 1 ⟹ ∂ A i j − 1 ∂ A k l = − A i k − 1 A l j − 1 {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{ik}^{-1}~T_{kl}~A_{lj}^{-1}\implies {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-A_{ik}^{-1}~A_{lj}^{-1}} ∂ ∂ A ( A − T ) : T = − A − T ⋅ T T ⋅ A − T {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-{\textsf {T}}}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-{\textsf {T}}}\cdot {\boldsymbol {T}}^{\textsf {T}}\cdot {\boldsymbol {A}}^{-{\textsf {T}}}} ∂ A j i − 1 ∂ A k l T k l = − A j k − 1 T l k A l i − 1 ⟹ ∂ A j i − 1 ∂ A k l = − A l i − 1 A j k − 1 {\displaystyle {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{jk}^{-1}~T_{lk}~A_{li}^{-1}\implies {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}=-A_{li}^{-1}~A_{jk}^{-1}} A {\displaystyle {\boldsymbol {A}}} ∂ A i j − 1 ∂ A k l = − 1 2 ( A i k − 1 A j l − 1 + A i l − 1 A j k − 1 ) {\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-{\cfrac {1}{2}}\left(A_{ik}^{-1}~A_{jl}^{-1}+A_{il}^{-1}~A_{jk}^{-1}\right)}
Prueba Recuerde que ∂ 1 ∂ A : T = 0 {\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
Desde entonces , podemos escribir A − 1 ⋅ A = 1 {\displaystyle {\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}={\boldsymbol {\mathit {1}}}} ∂ ∂ A ( A − 1 ⋅ A ) : T = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}\right):{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
Utilizando la regla del producto para tensores de segundo orden ∂ ∂ S [ F 1 ( S ) ⋅ F 2 ( S ) ] : T = ( ∂ F 1 ∂ S : T ) ⋅ F 2 + F 1 ⋅ ( ∂ F 2 ∂ S : T ) {\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
obtenemos
o, ∂ ∂ A ( A − 1 ⋅ A ) : T = ( ∂ A − 1 ∂ A : T ) ⋅ A + A − 1 ⋅ ( ∂ A ∂ A : T ) = 0 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}):{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}+{\boldsymbol {A}}^{-1}\cdot \left({\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)={\boldsymbol {\mathit {0}}}} ( ∂ A − 1 ∂ A : T ) ⋅ A = − A − 1 ⋅ T {\displaystyle \left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}}
Por lo tanto, ∂ ∂ A ( A − 1 ) : T = − A − 1 ⋅ T ⋅ A − 1 {\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}}
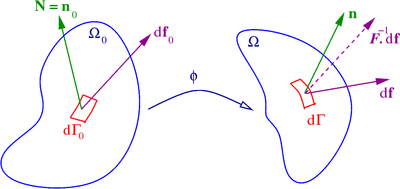
Integración por partes Dominio , su límite y la unidad normal exterior Ω {\displaystyle \Omega } Γ {\displaystyle \Gamma } n {\displaystyle \mathbf {n} } Otra operación importante relacionada con las derivadas tensoriales en la mecánica de medios continuos es la integración por partes. La fórmula para la integración por partes se puede escribir como ∫ Ω F ⊗ ∇ G d Ω = ∫ Γ n ⊗ ( F ⊗ G ) d Γ − ∫ Ω G ⊗ ∇ F d Ω {\displaystyle \int _{\Omega }{\boldsymbol {F}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes ({\boldsymbol {F}}\otimes {\boldsymbol {G}})\,d\Gamma -\int _{\Omega }{\boldsymbol {G}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {F}}\,d\Omega }
donde y son campos tensoriales diferenciables de orden arbitrario, es la unidad normal exterior al dominio sobre el que se definen los campos tensoriales, representa un operador de producto tensorial generalizado y es un operador de gradiente generalizado. Cuando es igual al tensor identidad, obtenemos el teorema de divergencia F {\displaystyle {\boldsymbol {F}}} G {\displaystyle {\boldsymbol {G}}} n {\displaystyle \mathbf {n} } ⊗ {\displaystyle \otimes } ∇ {\displaystyle {\boldsymbol {\nabla }}} F {\displaystyle {\boldsymbol {F}}} ∫ Ω ∇ G d Ω = ∫ Γ n ⊗ G d Γ . {\displaystyle \int _{\Omega }{\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes {\boldsymbol {G}}\,d\Gamma \,.}
Podemos expresar la fórmula de integración por partes en notación de índice cartesiano como ∫ Ω F i j k . . . . G l m n . . . , p d Ω = ∫ Γ n p F i j k . . . G l m n . . . d Γ − ∫ Ω G l m n . . . F i j k . . . , p d Ω . {\displaystyle \int _{\Omega }F_{ijk....}\,G_{lmn...,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ijk...}\,G_{lmn...}\,d\Gamma -\int _{\Omega }G_{lmn...}\,F_{ijk...,p}\,d\Omega \,.}
Para el caso especial donde la operación del producto tensorial es una contracción de un índice y la operación del gradiente es una divergencia, y ambos y son tensores de segundo orden, tenemos F {\displaystyle {\boldsymbol {F}}} G {\displaystyle {\boldsymbol {G}}} ∫ Ω F ⋅ ( ∇ ⋅ G ) d Ω = ∫ Γ n ⋅ ( G ⋅ F T ) d Γ − ∫ Ω ( ∇ F ) : G T d Ω . {\displaystyle \int _{\Omega }{\boldsymbol {F}}\cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {G}})\,d\Omega =\int _{\Gamma }\mathbf {n} \cdot \left({\boldsymbol {G}}\cdot {\boldsymbol {F}}^{\textsf {T}}\right)\,d\Gamma -\int _{\Omega }({\boldsymbol {\nabla }}{\boldsymbol {F}}):{\boldsymbol {G}}^{\textsf {T}}\,d\Omega \,.}
En notación de índice, ∫ Ω F i j G p j , p d Ω = ∫ Γ n p F i j G p j d Γ − ∫ Ω G p j F i j , p d Ω . {\displaystyle \int _{\Omega }F_{ij}\,G_{pj,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ij}\,G_{pj}\,d\Gamma -\int _{\Omega }G_{pj}\,F_{ij,p}\,d\Omega \,.}
Véase también
Referencias ^ JC Simo y TJR Hughes, 1998, Inelasticidad computacional , Springer ^ JE Marsden y TJR Hughes, 2000, Fundamentos matemáticos de la elasticidad , Dover. ^ RW Ogden, 2000, Deformaciones elásticas no lineales , Dover. ^ ab Hjelmstad, Keith (2004). Fundamentos de mecánica estructural . Springer Science & Business Media. pág. 45. ISBN 9780387233307 
![{\displaystyle {\frac {\parcial f}{\parcial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/308eadd1b18b96a60ef33e8df365bccc97f0faea)
![{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8835d592f0ae810b9b57fa81f345a4850f1f1ce)
![{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3916392ebeebca9ebddb31e76edb1c9f8c08b586)
![{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2072ee23ca460f6f32851f397b5879a47033c3b)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} &=\left.{\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(x_{1}+\alpha c_{1},x_{2}+\alpha c_{2},x_{3}+\alpha c_{3})\right|_{\alpha =0}\equiv \left.{\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(y_{1},y_{2},y_{3})\right|_{\alpha =0}\\&=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~{\cfrac {\partial y_{1}}{\partial \alpha }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{2}}}~{\cfrac {\partial y_{2}}{\partial \alpha }}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~{\cfrac {\partial y_{3}}{\partial \alpha }}\right]_{\alpha =0}=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial y_{3}}}~c_{3}\right]_{\alpha =0}\\&={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{1}}}~c_{1}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{2}}}~c_{2}+{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{3}}}~c_{3}\equiv {\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~c_{i}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}~(\mathbf {e} _{i}\cdot \mathbf {c} )=\left[{\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i}\right]\cdot \mathbf {c} \qquad \square \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b848452c7189fb099eb1dadf20cd7c167dd4d2e)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad &{\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r} +{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{ \partial z}}~\mathbf {e} _{z}\\{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{r}}{ \theta parcial }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{r}}{\partial z} }~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{\theta }}{\partial r}}~\ mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \ theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{z}}{ \partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial v_{z}}{\ parcial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e } _{z}\otimes \mathbf {e} _{z}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}} {\parcial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{ \frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }} {\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}} \left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\parcial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1} {r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf { e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}} ~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partialS_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{ \frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\ derecha]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\ parcial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz }\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac { \partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{\partial r}}~\ mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[ {\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta } \otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \ mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{ \partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta } }{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta } \\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e } _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta } }{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta } \\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e } _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f19df7af85562767daf41dcce9042d343a7cf917)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i} \cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~ \mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&= {\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii} ~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~ \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/864380cd0a82178354a80ee58109fc0519c149ba)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~S^{lj}+\Gamma _{il}^{j}~S^{il}\right]~\mathbf {b} _{j}\\[8pt]&=\left[{\cfrac {\partial S_{~j}^{i}}{\partial q^{i}}}+\Gamma _{il}^{i}~S_{~j}^{l}-\Gamma _{ij}^{l}~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{\partial q^{k}}}-\Gamma _{ik}^{l}~S_{l} ^{~j}+\Gamma _{kl}^{j}~S_{i}^{~l}\right]~g^{ik}~\mathbf {b} _{j}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85fad1b0228d189867b87f1d770c3968e4394860)
![{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8cd23836a8e6cc12150592c3964d95d6a3f94e9)
![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a229cf1ec76d8d0d6c4ebf0e55e24a9289524d0f)
![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}&=\left.{\cfrac {d}{d\alpha }}\det({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right|_{\alpha =0}\\&=\left.{\cfrac {d}{d\alpha }}\det \left[\alpha ~{\boldsymbol {A}}\left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}\\&=\left.{\cfrac {d}{d\alpha }}\left[\alpha ^{3}~\det({\boldsymbol {A}})~\det \left({\cfrac {1}{\alpha }}~{\boldsymbol {\mathit {I}}}+{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right]\right|_{\alpha =0}.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a280dfed26c159c4b698ac9db1c9e7b4ff9ce7c)
![{\displaystyle {\begin{aligned}{\frac {\partial f}{\partial {\boldsímbolo {A}}}}:{\boldsímbolo {T}}&=\left.{\cfrac {d}{d\alpha }}\left[\alpha ^{3}~\det({\boldsímbolo {A}})~\left({\cfrac {1}{\alpha ^{3}}}+I_{1}\left({\boldsímbolo {A}}^{-1}\cdot {\boldsímbolo {T}}\right)~{\cfrac {1}{\alpha ^{2}}}+I_{2}\left({\boldsímbolo {A}}^{-1}\cdot {\boldsímbolo {T}}\right)~{\cfrac {1}{\alpha }}+I_{3}\left({\boldsímbolo {A}}^{-1}\cdot {\boldsymbol {T}}\right)\right)\right]\right|_{\alpha =0}\\&=\left.\det({\boldsymbol {A}})~{\cfrac {d}{d\alpha }}\left[1+I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha +I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}+I_{3}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{3}\right]\right|_{\alpha =0}\\&=\left.\det({\boldsymbol {A}})~\left[I_{1}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}})+2~I_{2}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha +3~I_{3}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~\alpha ^{2}\right]\right|_{\alpha =0}\\&=\det({\boldsymbol {A}})~I_{1}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\right)~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc69b4584b67f7559a984e1c3d5dfa5b0f663c83)
![{\displaystyle {\frac {\partial f}{\partial {\boldsímbolo {A}}}}:{\boldsímbolo {T}}=\det({\boldsímbolo {A}})~{\text{tr}}\left({\boldsímbolo {A}}^{-1}\cdot {\boldsímbolo {T}}\right)=\det({\boldsímbolo {A}})~\left[{\boldsímbolo {A}}^{-1}\right]^{\textsf {T}}:{\boldsímbolo {T}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfbbc8e843ee49828711668186ed4e5faa93384)
![{\displaystyle {\frac {\parcial f}{\parcial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf1328c61318cc48aa33f6c0b580b55e268f7ebe)
![{\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A}})&={\frac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb5f440de0bb33a949001c6bef13f9f829fb1a42)
![{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19cf1ad5bce9774bf510c8818f4b90e32c4f2640)
![{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9dd4a16751516c5e316be643e40ce0babf1c1df)
![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be1b29969a25190e4efad41db9d76f11e8a8079)
![{\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{alineado}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a4ad226ea72ae236eaddfe419007ff6de53d55d)
![{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3993a79ec1f95da1b9e188243300861ee7ee2e45)
![{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/782fb846f7870890e72cda9dbeba6e80dfc064b0)
![{\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d9d08c98dc866bcc330678342ca3c391da0042a)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6174aae82fa111cbe2235a21c275bb7bc0e243b4)
![{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8169e3ea8470a718a349e0d8a73e1fb7c162914)
![{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4cf9341eabbe69c48f4ff85db571b84c8b2c318)
![{\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73a25e5e0ee3f8a2f287da104d5f72d8342899b9)
