En matemáticas , la secuencia de mirar y decir es la secuencia de números enteros que comienza de la siguiente manera:
Para generar un miembro de la secuencia a partir del miembro anterior, lea los dígitos del miembro anterior, contando el número de dígitos en grupos del mismo dígito. Por ejemplo:
La secuencia de mirar y decir fue analizada por John Conway [1] después de que uno de sus alumnos se la presentara en una fiesta. [2] [3]
La idea de la secuencia de mirar y decir es similar a la de la codificación de longitud de ejecución .
Si comienza con cualquier dígito d del 0 al 9, d permanecerá indefinidamente como el último dígito de la secuencia. Para cualquier d distinto de 1, la secuencia comienza de la siguiente manera:
Ilan Vardi ha llamado a esta secuencia, comenzando con d = 3, la secuencia de Conway (secuencia A006715 en la OEIS ). (para d = 2, ver OEIS : A006751 ) [4]
La secuencia crece indefinidamente. De hecho, cualquier variante definida comenzando con un número de semilla entero diferente (eventualmente) también crecerá indefinidamente, excepto la secuencia degenerada : 22, 22, 22, 22, ... que permanece del mismo tamaño (secuencia A010861 en el OEIS ) [5]
En la secuencia no aparecen dígitos distintos de 1, 2 y 3, a menos que el número inicial contenga dicho dígito o una serie de más de tres del mismo dígito. [5]
El teorema cosmológico de Conway afirma que cada secuencia finalmente se divide ("se desintegra") en una secuencia de "elementos atómicos", que son subsecuencias finitas que nunca más interactúan con sus vecinos. Hay 92 elementos que contienen únicamente los dígitos 1, 2 y 3, a los que John Conway nombró en honor a los 92 elementos químicos naturales hasta el uranio , llamando a la secuencia audioactiva . También hay dos elementos " transuránicos " (Np y Pu) para cada dígito que no sea 1, 2 y 3. [5] [6] A continuación se muestra una tabla de todos esos elementos:
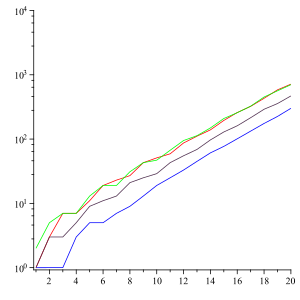
Los términos eventualmente crecen en longitud alrededor de un 30% por generación. En particular, si L n denota el número de dígitos del n -ésimo miembro de la secuencia, entonces el límite de la relación existe y está dado por
donde λ = 1,303577269034... (secuencia A014715 en la OEIS ) es un número algebraico de grado 71. [5] Este hecho fue demostrado por Conway, y la constante λ se conoce como constante de Conway . El mismo resultado también es válido para cada variante de la secuencia que comienza con cualquier semilla distinta de 22.
La constante de Conway es la única raíz real positiva del siguiente polinomio (secuencia A137275 en la OEIS ):
Este polinomio se dio correctamente en el artículo original de Conway en Eureka , [1] pero en la versión reimpresa en el libro editado por Cover y Gopinath [1] el término se imprimió incorrectamente con un signo menos delante. [7]
La secuencia de mirar y decir también se conoce popularmente como secuencia numérica de Morris , en honor al criptógrafo Robert Morris , y el acertijo "¿Cuál es el siguiente número en la secuencia 1, 11, 21, 1211, 111221?" A veces se lo conoce como el huevo del cuco , según una descripción de Morris en el libro de Clifford Stoll El huevo del cuco . [8] [9]
Hay muchas variaciones posibles de la regla utilizada para generar la secuencia de mirar y decir. Por ejemplo, para formar el "patrón de guisante", se lee el término anterior y se cuentan todas las instancias de cada dígito, enumeradas en el orden de su primera aparición, no solo las que ocurren en un bloque consecutivo. Entonces, comenzando con la semilla 1, el patrón de guisantes continúa 1, 11 ("un 1"), 21 ("dos 1"), 1211 ("un 2 y un 1"), 3112 ("tres 1 y un 2") , 132112 ("un 3, dos 1 y un 2"), 311322 ("tres 1, un 3 y dos 2"), etc. Esta versión del patrón de guisante eventualmente forma un ciclo con los dos términos "atómicos" 23322114 y 32232114.
También son posibles otras versiones del patrón de guisantes; por ejemplo, en lugar de leer los dígitos como aparecen por primera vez, se podrían leer en orden ascendente. En este caso, el término que sigue a 21 sería 1112 ("un 1, un 2") y el término que sigue a 3112 sería 211213 ("dos 1, un 2 y un 3").
Estas secuencias difieren en varios aspectos notables de la secuencia de mirar y decir. En particular, a diferencia de las secuencias de Conway, un término dado del patrón de guisante no define de forma única el término anterior. Además, para cualquier semilla, el patrón de guisante produce términos de longitud limitada: este límite normalmente no excederá 2 × Radix + 2 dígitos (22 dígitos para decimal : base = 10 ) y solo puede exceder 3 × dígitos de Radix (30 dígitos para base decimal). ) de longitud para semillas iniciales largas, degeneradas (secuencia de "100 unos", etc.). Para estos casos extremos, los elementos individuales de las secuencias decimales se asientan inmediatamente en una permutación de la forma a 0 b 1 c 2 d 3 e 4 f 5 g 6 h 7 i 8 j 9 donde aquí las letras a – j son marcadores de posición para el recuento de dígitos del elemento de secuencia anterior.
Dado que la secuencia es infinita y la longitud de cada elemento está limitada, eventualmente debe repetirse, debido al principio de casillero . Como consecuencia, las secuencias del patrón de guisante siempre son eventualmente periódicas .