Tipo de carga de partículas que se encuentra en el Modelo Estándar
En física de partículas , la hipercarga (un acrónimo de hiperónico y carga ) Y de una partícula es un número cuántico conservado bajo la interacción fuerte . El concepto de hipercarga proporciona un único operador de carga que explica las propiedades de isospín , carga eléctrica y sabor . La hipercarga es útil para clasificar hadrones ; la hipercarga débil, de nombre similar, tiene un papel análogo en la interacción electrodébil .
Definición
La hipercarga es uno de los dos números cuánticos del modelo SU(3) de hadrones , junto con el isospín I 3 . El isospín por sí solo fue suficiente para dos sabores de quarks , a saber:túyd—mientras que en la actualidad se conocen seis sabores de quarks.
Los diagramas de peso SU(3) (ver abajo) son bidimensionales, con coordenadas que hacen referencia a dos números cuánticos: I 3 (también conocido como I z ), que es el componente z del isospín, e Y , que es la hipercarga (definida por la extrañeza S , el encanto C , el fondo B′ , la cima T′ y el número bariónico B ). Matemáticamente, la hipercarga es [1]

Las interacciones fuertes conservan la hipercarga (y la hipercarga débil ), pero las interacciones débiles no .
Relación con la carga eléctrica y el isospín
La fórmula de Gell-Mann–Nishijima relaciona el isospín y la carga eléctrica

donde I 3 es el tercer componente del isospín y Q es la carga de la partícula.
El isospín crea multipletes de partículas cuya carga promedio está relacionada con la hipercarga por:

ya que la hipercarga es la misma para todos los miembros de un multiplete y el promedio de los valores I 3 es 0.
Estas definiciones en su forma original sólo son válidas para los tres quarks más ligeros.
Modelo SU(3) en relación con la hipercarga
El modelo SU(2) tiene multipletes caracterizados por un número cuántico J , que es el momento angular total . Cada multiplete consta de 2 J + 1 subestados con valores de J z igualmente espaciados , formando una disposición simétrica que se observa en los espectros atómicos y el isospín. Esto formaliza la observación de que no se observaron ciertas desintegraciones bariónicas fuertes, lo que llevó a la predicción de la masa, la extrañeza y la carga de la
Ohmio−
barión .
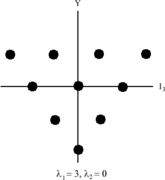
SU(3) tiene supermultipletes que contienen multipletes SU(2). SU(3) ahora necesita dos números para especificar todos sus subestados, que se denotan por λ 1 y λ 2 .
( λ 1 + 1) especifica el número de puntos en el lado superior del hexágono, mientras que ( λ 2 + 1) especifica el número de puntos en el lado inferior.
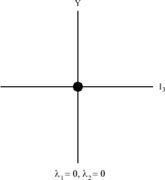
Diagrama de peso singlete SU(3) , donde Y es la hipercarga e I 3 es el tercer componente del isospín.
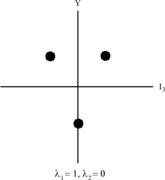
Diagrama de peso del triplete SU(3)
Diagrama de pesos de septeto, octeto y noneto SU(3) Nótese la similitud con ambos gráficos de la derecha. El número utilizado para describir el diagrama de pesos depende de si las partículas que ocupan el centro del diagrama tienen uno, dos o tres nombres distintos.
Los mesones de espín 0 forman un
noneto . K: kaon , π: pion , η:
mesón eta .
El
octeto del giro de la luz -
1/2 bariones descritos en SU(3). n:
neutrón , p:
protón , Λ:
barión Lambda , Σ:
barión Sigma , Ξ:
barión Xi .
Diagrama de peso del decuplete SU(3) Nótese la similitud con el gráfico de la derecha.
Una combinación de tres
quarks up, down o strange con un giro total de
3/2 forman el llamado
decuplete bariónico . Los seis inferiores son hiperones.
S :
extrañeza ,
Q :
carga eléctrica .
Ejemplos
- El grupo de nucleones ( protones con Q = +1 y neutrones con Q = 0 ) tienen una carga promedio de + +1/2 , por lo que ambos tienen hipercarga Y = 1 (ya que el número bariónico B = +1 y S = C = B′ = T′ = 0 ). De la fórmula de Gell-Mann–Nishijima sabemos que el protón tiene isospín I 3 = + +1/2 , mientras que el neutrón tiene I 3 = − +1/2 .
- Esto también funciona para los quarks : para el quark up , con una carga de ++2/3 , y un I 3 de ++1/2 , deducimos una hipercarga de 1/3 , debido a su número bariónico (ya que tres quarks forman un barión, cada quark tiene un número bariónico de ++1/3 ).
- Para un quark extraño , con carga eléctrica −+1/3 , un número bariónico de ++1/3 , y extrañeza −1, obtenemos una hipercarga Y = − +2/3 , por lo que deducimos que I 3 = 0 . Eso significa que un quark strange forma su propio singlete de isospín (lo mismo ocurre con los quarks charm , bottom y top ), mientras que up y down constituyen un doblete de isospín.
- Todos los demás quarks tienen hipercarga Y = 0 .
Obsolescencia práctica
La hipercarga fue un concepto desarrollado en la década de 1960 para organizar grupos de partículas en el " zoológico de partículas " y desarrollar leyes de conservación ad hoc basadas en sus transformaciones observadas. Con la llegada del modelo de quarks , ahora es obvio que la hipercarga fuerte, Y , es la siguiente combinación de los números de up ( n u ), down ( n d ), strange ( n s ), charm ( n c ), top ( n t ) y bottom ( n b ):

En las descripciones modernas de la interacción hadrónica , se ha vuelto más obvio dibujar diagramas de Feynman que trazan los quarks constituyentes individuales (que se conservan) que componen los bariones y mesones en interacción , en lugar de molestarse en contar los números cuánticos de hipercarga fuerte. Sin embargo, la hipercarga débil sigue siendo una parte esencial para comprender la interacción electrodébil .
Referencias
- ^ Particle Data Group, ed. (2022), 15. Modelo de quarks (PDF)
- Semat, Henry; Albright, John R. (1984). Introducción a la física atómica y nuclear . Chapman y Hall. ISBN 978-0-412-15670-0.