
Haidao Suanjing (海島算經; El manual matemático de la isla ) fue escrito por el matemático chino Liu Hui de laera de los Tres Reinos (220-280) como una extensión del capítulo 9 de Los nueve capítulos sobre el arte matemático . [1] Durante la dinastía Tang , este apéndice se extrajo de Los nueve capítulos sobre el arte matemático como un libro separado, titulado Haidao suanjing ( Manual matemático de la isla del mar ), llamado así por el problema n.° 1 "Mirar una isla del mar". En la época de la dinastía Tang temprana, Haidao Suanjing fue seleccionado en uno de Los diez cánones computacionales como los textos matemáticos oficiales para los exámenes imperiales en matemáticas.

Este libro contenía muchos problemas prácticos de topografía utilizando geometría. Esta obra proporcionaba instrucciones detalladas sobre cómo medir distancias y alturas con jalones de topógrafo altos y barras horizontales fijadas en ángulo recto a ellos. Las unidades de medida eran
El cálculo se realizó con el método de cálculo de Rod de valor posicional decimal .
Liu Hui utilizó su teorema del rectángulo en el triángulo rectángulo como base matemática para la encuesta. La configuración se muestra a la derecha. Al invocar su principio de "complemento interno-externo", demostró que el área de dos rectángulos inscritos en los dos triángulos rectángulos complementarios tiene el mismo área, por lo tanto

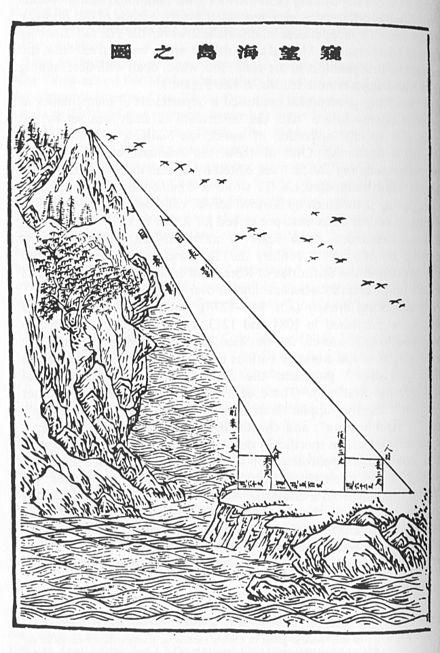
Ahora estamos inspeccionando una isla marina. Coloque dos postes de 3 zhang a 1000 pasos de distancia; deje que los dos postes y la isla estén en línea recta. Retroceda 123 pasos desde el poste delantero . Con la vista a nivel del suelo, la punta del poste está en línea recta con el pico de la isla. Retroceda 127 pasos desde el poste trasero. La vista a nivel del suelo también está alineada con la punta del poste y la punta de la isla. ¿Cuál es la altura de la isla y cuál es la distancia hasta el poste?
Respuesta: La altura de la isla es de 4 li y 55 escalones , y está a 102 li y 150 escalones desde el polo.
Método: Sea el numerador igual a la altura del poste multiplicada por la separación de los postes, sea el denominador la diferencia de los desfases, sume el cociente a la altura del poste para obtener la altura de la isla.
Como la distancia del poste delantero a la isla no se podía medir directamente, Liu Hui colocó dos postes de la misma altura a una distancia conocida entre sí y realizó dos mediciones. El poste estaba perpendicular al suelo, a la vista desde el nivel del suelo cuando la punta del poste estaba en línea recta con la cima de la isla, la distancia del ojo al poste se llamaba desplazamiento frontal = , de manera similar, el desplazamiento posterior = , diferencia de desplazamientos = .
Utilizando su principio de inscribir un rectángulo en un triángulo rectángulo para y , obtuvo:

Un pino de altura desconocida crece en la colina. Coloque dos postes de 2 zhang cada uno, uno al frente y otro en la parte trasera, a 50 pasos de distancia entre ellos. Deje que el poste trasero se alinee con el poste delantero. Retroceda 7 pasos y 4 chi , observe la punta del pino desde el suelo hasta que se alinee en línea recta con la punta del poste. Luego observe el tronco del árbol, la línea de visión intersecta los postes a 2 chi y 8 cun desde su punta. Retroceda 8 pasos y 5 chi desde el poste trasero, la vista desde el suelo también se alinea con la copa del árbol y la copa del poste. ¿Cuál es la altura del pino y cuál es su distancia desde el poste?
Respuesta: la altura del pino es de 12 zhang 2 chi 8 cun , la distancia de la montaña desde el poste es de 1 li y (28 + 4/7) pasos .
Método: sea el numerador el producto de la separación de los polos y la intersección desde la punta del polo, sea el denominador la diferencia de los desfases. Sume la altura del polo al cociente para obtener la altura del pino.

Estamos viendo desde el sur una ciudad cuadrada de tamaño desconocido. Coloca un gnomo al este y un poste al oeste, separados por 6 zhang , unidos con una cuerda a la altura de los ojos. Deja que el poste este se alinee con las esquinas NE y SE. Retrocede 5 pasos desde el gnomo al norte, observa la esquina NO de la ciudad, la línea de visión interseca la cuerda a 2 zhang 2 chi y 6,5 cun desde el extremo este. Retrocede 13 pasos y 2 chi hacia el norte , observa la esquina NO de la ciudad, la línea de visión se alinea con el polo oeste. ¿Cuál es la longitud de la ciudad cuadrada y cuál es su distancia al poste?
Respuesta: La longitud de la ciudad cuadrada es de 3 li , 43 y 3/4 pasos ; la distancia de la ciudad al polo es de 4 li y 45 pasos .

El misionero cristiano protestante británico del siglo XIX Alexander Wylie , en su artículo "Jottings on the Sciences of Chinese Mathematics" publicado en North China Herald en 1852, fue la primera persona en introducir el Manual matemático de Sea Island en Occidente. En 1912, el historiador matemático japonés Yoshio Mikami publicó El desarrollo de las matemáticas en China y Japón , el capítulo 5 estuvo dedicado a este libro. [2] Un matemático francés tradujo el libro al francés en 1932. [1] En 1986, Ang Tian Se y Frank Swetz tradujeron el haidao al inglés.
Después de comparar el desarrollo de la topografía en China y Occidente, Frank Swetz concluyó que "en los esfuerzos de la topografía matemática, los logros de China superaron a los alcanzados en Occidente en unos mil años". [3]