En criptografía , un HMAC (que a veces se expande como código de autenticación de mensajes con clave hash o código de autenticación de mensajes basado en hash ) es un tipo específico de código de autenticación de mensajes (MAC) que implica una función hash criptográfica y una clave criptográfica secreta. Al igual que con cualquier MAC, se puede utilizar para verificar simultáneamente tanto la integridad de los datos como la autenticidad de un mensaje. Un HMAC es un tipo de función hash con clave que también se puede utilizar en un esquema de derivación de claves o en un esquema de estiramiento de claves.
HMAC puede proporcionar autenticación mediante un secreto compartido en lugar de usar firmas digitales con criptografía asimétrica . Evita la necesidad de una infraestructura de clave pública compleja al delegar el intercambio de claves a las partes que se comunican, quienes son responsables de establecer y usar un canal confiable para acordar la clave antes de la comunicación.
Cualquier función hash criptográfica, como SHA-2 o SHA-3 , puede utilizarse en el cálculo de un HMAC; el algoritmo MAC resultante se denomina HMAC- x , donde x es la función hash utilizada (por ejemplo, HMAC-SHA256 o HMAC-SHA3-512). La solidez criptográfica del HMAC depende de la solidez criptográfica de la función hash subyacente, del tamaño de su salida hash y del tamaño y la calidad de la clave. [1]
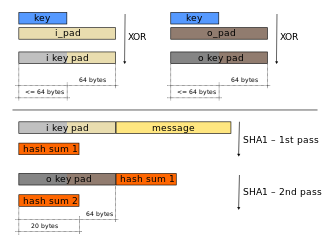
HMAC utiliza dos pasos de cálculo de hash. Antes de cada paso, se utiliza la clave secreta para derivar dos claves: interna y externa. A continuación, el primer paso del algoritmo hash produce un hash interno derivado del mensaje y la clave interna. El segundo paso produce el código HMAC final derivado del resultado del hash interno y la clave externa. De este modo, el algoritmo proporciona una mejor inmunidad contra los ataques de extensión de longitud .
Una función hash iterativa (que utiliza la construcción Merkle–Damgård ) divide un mensaje en bloques de un tamaño fijo y los itera con una función de compresión . Por ejemplo, SHA-256 opera en bloques de 512 bits. El tamaño de la salida de HMAC es el mismo que el de la función hash subyacente (por ejemplo, 256 y 512 bits en el caso de SHA-256 y SHA3-512, respectivamente), aunque se puede truncar si se desea.
HMAC no cifra el mensaje. En su lugar, el mensaje (cifrado o no) debe enviarse junto con el hash HMAC. Las partes que tengan la clave secreta volverán a cifrar el mensaje y, si es auténtico, los hashes recibidos y calculados coincidirán.
La definición y el análisis de la construcción HMAC se publicaron por primera vez en 1996 en un artículo de Mihir Bellare , Ran Canetti y Hugo Krawczyk , [1] [2] y también escribieron RFC 2104 en 1997. [3] : §2 El artículo de 1996 también definió una variante anidada llamada NMAC (Nested MAC). FIPS PUB 198 generaliza y estandariza el uso de HMAC. [4] HMAC se utiliza dentro de los protocolos IPsec , [2] SSH y TLS y para JSON Web Tokens .
Esta definición está tomada del RFC 2104:
dónde
El siguiente pseudocódigo demuestra cómo se puede implementar HMAC. El tamaño del bloque es de 512 bits (64 bytes) cuando se utiliza una de las siguientes funciones hash: SHA-1, MD5, RIPEMD-128. [3] : §2
La función hmac se ingresa: clave: Bytes // Matriz de bytes mensaje: Bytes // Matriz de bytes a codificar hash: Función // La función hash a utilizar (por ejemplo, SHA-1) blockSize: Entero // El tamaño del bloque de la función hash (por ejemplo, 64 bytes para SHA-1) outputSize: Entero // El tamaño de salida de la función hash (por ejemplo, 20 bytes para SHA-1) // Calcular la clave del tamaño del bloque block_sized_key = calculateBlockSizedKey(clave, hash, blockSize) o_key_pad ← block_sized_key xor [0x5c blockSize] // Tecla con relleno exterior i_key_pad ← block_sized_key xor [0x36 blockSize] // Tecla con relleno interior devuelve hash(o_key_pad ∥ hash(i_key_pad ∥ mensaje))La función calculateBlockSizedKey se ingresa: key: Bytes // Matriz de bytes hash: Función // La función hash a utilizar (por ejemplo, SHA-1) blockSize: Entero // El tamaño del bloque de la función hash (por ejemplo, 64 bytes para SHA-1) // Las claves más largas que blockSize se acortan mediante hash si (length(key) > blockSize) entonces clave = hash(clave) // Las claves más cortas que blockSize se rellenan hasta blockSize rellenando con ceros a la derecha if (length(key) < blockSize) then return Pad(key, blockSize) // Rellena la clave con ceros para que tenga una longitud de blockSize en bytes tecla de retorno
El diseño de la especificación HMAC fue motivado por la existencia de ataques a mecanismos más triviales para combinar una clave con una función hash. Por ejemplo, uno podría asumir que la misma seguridad que proporciona HMAC podría lograrse con MAC = H ( clave ∥ mensaje ). Sin embargo, este método sufre de un defecto grave: con la mayoría de las funciones hash, es fácil añadir datos al mensaje sin conocer la clave y obtener otra MAC válida (" ataque de extensión de longitud "). La alternativa, añadir la clave utilizando MAC = H ( mensaje ∥ clave ), sufre del problema de que un atacante que puede encontrar una colisión en la función hash (sin clave) tiene una colisión en la MAC (ya que dos mensajes m1 y m2 que producen el mismo hash proporcionarán la misma condición de inicio a la función hash antes de que la clave añadida se convierta en hash, por lo tanto, el hash final será el mismo). Usar MAC = H ( clave ∥ mensaje ∥ clave ) es mejor, pero varios documentos de seguridad han sugerido vulnerabilidades con este enfoque, incluso cuando se utilizan dos claves diferentes. [1] [7] [8]
No se han encontrado ataques de extensión conocidos contra la especificación HMAC actual, que se define como H ( clave ∥ H ( clave ∥ mensaje )) porque la aplicación externa de la función hash enmascara el resultado intermedio del hash interno. Los valores de ipad y opad no son críticos para la seguridad del algoritmo, pero se definieron de tal manera que tengan una gran distancia de Hamming entre sí y, por lo tanto, las claves internas y externas tendrán menos bits en común. La reducción de seguridad de HMAC requiere que sean diferentes en al menos un bit. [ cita requerida ]
La función hash Keccak , que fue seleccionada por NIST como ganadora de la competencia SHA-3 , no necesita este enfoque anidado y puede usarse para generar una MAC simplemente anteponiendo la clave al mensaje, ya que no es susceptible a ataques de extensión de longitud. [9]
La fuerza criptográfica del HMAC depende del tamaño de la clave secreta que se utiliza y de la seguridad de la función hash subyacente utilizada. Se ha demostrado que la seguridad de una construcción HMAC está directamente relacionada con las propiedades de seguridad de la función hash utilizada. El ataque más común contra los HMAC es la fuerza bruta para descubrir la clave secreta. Los HMAC se ven sustancialmente menos afectados por las colisiones que sus algoritmos hash subyacentes por sí solos. [2] [10] [11] En particular, Mihir Bellare demostró que HMAC es una función pseudoaleatoria (PRF) bajo el único supuesto de que la función de compresión es una PRF. [12] Por lo tanto, HMAC-MD5 no sufre de las mismas debilidades que se han encontrado en MD5. [13]
RFC 2104 requiere que "las claves más largas que B bytes se conviertan primero en hashes utilizando H ", lo que lleva a una pseudocolisión confusa: si la clave es más larga que el tamaño del bloque hash (por ejemplo, 64 bytes para SHA-1), entonces HMAC(k, m)se calcula como HMAC(H(k), m). Esta propiedad a veces se plantea como una posible debilidad de HMAC en escenarios de hash de contraseñas: se ha demostrado que es posible encontrar una cadena ASCII larga y un valor aleatorio cuyo hash también será una cadena ASCII, y ambos valores producirán la misma salida HMAC. [14] [15] [16]
En 2006, Jongsung Kim, Alex Biryukov , Bart Preneel y Seokhie Hong demostraron cómo distinguir HMAC con versiones reducidas de MD5 y SHA-1 o versiones completas de HAVAL , MD4 y SHA-0 de una función aleatoria o HMAC con una función aleatoria. Los diferenciadores diferenciales permiten a un atacante idear un ataque de falsificación en HMAC. Además, los diferenciadores diferenciales y rectangulares pueden conducir a ataques de segunda preimagen . HMAC con la versión completa de MD4 se puede falsificar con este conocimiento. Estos ataques no contradicen la prueba de seguridad de HMAC, pero brindan información sobre HMAC basada en funciones hash criptográficas existentes. [17]
En 2009, Xiaoyun Wang et al. presentaron un ataque de distinción en HMAC-MD5 sin utilizar claves relacionadas. Puede distinguir una instanciación de HMAC con MD5 de una instanciación con una función aleatoria con 2 97 consultas con probabilidad 0,87. [18]
En 2011 se publicó un RFC 6151 informativo para resumir las consideraciones de seguridad en MD5 y HMAC-MD5. Para HMAC-MD5, el RFC resume que, aunque la seguridad de la función hash MD5 en sí está gravemente comprometida, los "ataques a HMAC-MD5 conocidos actualmente no parecen indicar una vulnerabilidad práctica cuando se utiliza como código de autenticación de mensajes" , pero también agrega que "para un nuevo diseño de protocolo, no se debe incluir un conjunto de cifrados con HMAC-MD5" . [13]
En mayo de 2011, se publicó el RFC 6234, que detalla la teoría abstracta y el código fuente de los HMAC basados en SHA. [19]
A continuación se muestran algunos valores HMAC, asumiendo ASCII de 8 bits para la entrada y codificación hexadecimal para la salida:
HMAC_MD5("key", "El rápido zorro marrón salta sobre el perro perezoso") = 80070713463e7749b90c2dc24911e275HMAC_SHA1("clave", "El rápido zorro marrón salta sobre el perro perezoso") = de7c9b85b8b78aa6bc8a7a36f70a90701c9db4d9HMAC_SHA256("clave", "El rápido zorro marrón salta sobre el perro perezoso") = f7bc83f430538424b13298e6aa6fb143ef4d59a14946175997479dbc2d1a3cd8HMAC_SHA512("key", "El rápido zorro marrón salta sobre el perro perezoso") = b42af09057bac1e2d41708e48a902e09b5ff7f12ab428a4fe86653c73dd248fb82f948a549f7b791a5b41915ee4d1ec3935357e4e2317250d0372afa2ebeeb3a{{cite journal}}: Requiere citar revista |journal=( ayuda ){{cite journal}}: Requiere citar revista |journal=( ayuda )A diferencia de SHA-1 y SHA-2, Keccak no tiene la debilidad de la extensión de longitud, por lo que no necesita la construcción anidada HMAC. En cambio, el cálculo MAC se puede realizar simplemente anteponiendo la clave al mensaje.
Aunque no afecta a aplicaciones como HMAC, donde las colisiones no son importantes.
El ataque más fuerte conocido contra HMAC se basa en la frecuencia de colisiones de la función hash H ("ataque de cumpleaños") [PV, BCK2], y es totalmente impráctico para funciones hash mínimamente razonables.
Este artículo demuestra que HMAC es una
PRF
bajo el único supuesto de que la función de compresión es una PRF. Esto recupera una garantía basada en pruebas ya que ningún ataque conocido compromete la pseudoaleatoriedad de la función de compresión, y también ayuda a explicar la resistencia a los ataques que HMAC ha demostrado incluso cuando se implementa con funciones hash cuya resistencia a colisiones (débil) está comprometida.
{{cite journal}}: Requiere citar revista |journal=( ayuda ){{citation}}: CS1 maint: numeric names: authors list (link) Informativo. Se deja obsoleto el RFC 4634. Se actualiza el RFC 3174