En el campo matemático de la teoría de grafos , el grafo de escalera L n es un grafo plano , no dirigido, con 2 n vértices y 3 n – 2 aristas. [1]
El gráfico de escalera se puede obtener como el producto cartesiano de dos gráficos de trayectoria , uno de los cuales tiene solo una arista: L n ,1 = P n × P 2 . [2] [3]
Por construcción, el grafo de escalera L n es isomorfo al grafo de cuadrícula G 2, n y parece una escalera con n peldaños. Es hamiltoniano con circunferencia 4 (si n > 1 ) e índice cromático 3 (si n > 2 ).
El número cromático del gráfico de escalera es 2 y su polinomio cromático es .
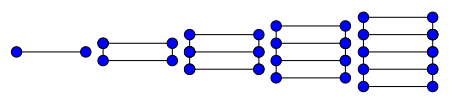
A veces se utiliza el término "gráfico de escalera" para el gráfico de escalera de n × P 2 , que es la unión gráfica de n copias del gráfico de ruta P 2 .

El grafo circular en escalera CL n se puede construir conectando los cuatro vértices de 2 grados de forma recta , o mediante el producto cartesiano de un ciclo de longitud n ≥ 3 y una arista. [4] En símbolos, CL n = C n × P 2 . Tiene 2 n nodos y 3 n aristas. Al igual que el grafo en escalera, es conexo , planar y hamiltoniano , pero es bipartito si y solo si n es par.
Los gráficos de escalera circular son los gráficos poliédricos de prismas, por lo que se les llama más comúnmente gráficos prismáticos .
Gráficas de escalera circular:
Conectando los cuatro vértices de 2 grados en forma transversal se crea un gráfico cúbico llamado escalera de Möbius.
