Las escalas transversales son una construcción geométrica de un instrumento científico que permite leer una graduación con un grado de precisión mayor. Su uso crea lo que a veces se denomina una escala diagonal , un instrumento de medición de ingeniería que se compone de un conjunto de líneas rectas paralelas que son cruzadas oblicuamente por otro conjunto de líneas rectas. Las escalas diagonales se utilizan para medir pequeñas fracciones de la unidad de medida . [1]
En la actualidad, las escalas transversales han sido sustituidas por escalas Vernier . Este método se basa en el teorema de la intersección (también conocido como teorema de Tales).
Las escalas transversales se utilizaban en una época en la que era difícil fabricar instrumentos con una graduación fina. Se empezaron a encontrar en instrumentos a principios del siglo XIV, pero se desconoce quién las inventó. En 1342, Levi Ben Gerson introdujo un instrumento llamado bastón de Jacob (al parecer inventado el siglo anterior por Jacob Ben Makir ) y describió el método de la escala transversal aplicado al mencionado instrumento. [2] [3]
Thomas Digges atribuyó erróneamente el descubrimiento de la escala transversal al navegante y explorador Richard Chancellor (citado por algunos autores como relojero y con otros nombres, entre ellos: Richard Chansler o Richard Kantzler). [4] [5] [6] [7] [8] [9] Su uso en instrumentos astronómicos solo comenzó a fines del siglo XVI. Tycho Brahe los utilizó e hizo mucho para popularizar la técnica. [10] [11] La técnica comenzó a desaparecer una vez que los nonios se volvieron comunes a fines del siglo XVIII, más de un siglo después de que Pierre Vernier introdujera la técnica.
En el intervalo entre las transversales y la escala de nonio, se utilizó el sistema nonius , desarrollado por Pedro Nunes . Sin embargo, nunca se utilizó de forma habitual. Tycho también utilizó métodos nonius, pero parece ser el único astrónomo destacado que lo hizo.
La escala diagonal se deriva de la palabra latina Diagonalis . La palabra latina se acuñó originalmente a partir de la palabra griega diagōnios , donde dia significa "a través" y gonios denota "esquinas". [1] [12]
La escala diagonal sigue el principio de triángulos similares donde una longitud corta se divide en un número de partes en las que los lados son proporcionales. [13] Dividido en el número requerido de partes iguales

Se utilizaron líneas transversales sobre graduaciones lineales. Se construyó una cuadrícula de líneas inmediatamente adyacente a las graduaciones lineales. Las líneas que se extendían por encima de las graduaciones formaban parte de la cuadrícula. El número de líneas perpendiculares a las líneas de graduación extendidas en la cuadrícula dependía del grado de finura que el fabricante del instrumento deseaba proporcionar.
Una cuadrícula de cinco líneas permitiría determinar la medida hasta un quinto de la división de una graduación. Una cuadrícula de diez líneas permitiría medir décimas. La distancia entre las líneas no es crítica siempre que la distancia sea exactamente uniforme. Cuanto mayor sea la distancia, mayor será la precisión.
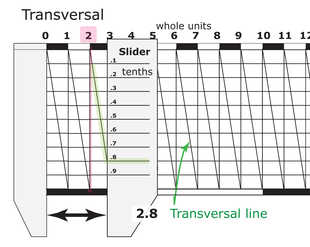
Como se ve en la ilustración de la derecha, una vez trazada la cuadrícula, se trazaron diagonales (líneas transversales) desde la esquina superior de una columna de la cuadrícula hasta la esquina inferior opuesta. Esta línea interseca las líneas transversales de la cuadrícula en intervalos iguales. Al utilizar un indicador como un cursor o una alidada , o al medir utilizando un par de divisores con puntos en la misma línea de cuadrícula horizontal, se determina el punto más cercano donde la transversal cruza la cuadrícula. Eso indica la fracción de la graduación para la medida.
En la ilustración, la lectura se indica mediante la línea roja vertical. Podría ser el borde de una alidada o un dispositivo similar. Dado que el cursor cruza la transversal más cercana a la cuarta línea de la cuadrícula desde arriba, la lectura (suponiendo que la línea de graduación larga más a la izquierda es 0,0) es 0,54.
La escala diagonal se utiliza en ingeniería para leer longitudes con mayor precisión, ya que representa una unidad en tres múltiplos diferentes en metros , centímetros y milímetros . [14] La escala diagonal es una parte importante en los dibujos de ingeniería . [15]
Las transversales circulares cumplen la misma función que las lineales, pero para arcos circulares. En este caso, la construcción de la cuadrícula es significativamente más complicada. Una cuadrícula rectangular no funcionará. Se debe crear una cuadrícula de líneas radiales y arcos circunferenciales. Además, una línea transversal lineal no dividirá la cuadrícula radial en segmentos iguales. Los segmentos de arcos circulares deben construirse como transversales para proporcionar las proporciones correctas.

Tycho Brahe creó una cuadrícula de líneas transversales formadas con secantes entre dos grupos de arcos que forman dos ramas graduadas. Las secantes se dibujan uniendo la división de una rama con la siguiente división de la otra rama, y así sucesivamente (véase la figura con el aumento de 2 grados del cuadrante de Tycho Brahe de 2 m de radio). [10]
Trazó, para cada grado, seis rectas transversales de modo alterno formando una “V” y cada transversal constaba de 9 puntos que la dividían en 10 partes, que multiplicadas por 6 dan 60 minutos. [16] Mientras que Abd al-Mun’im al ‘Âmilî (siglo XVI) las dibujó todas en la misma dirección (aunque su instrumento tiene menor precisión). [17]
El método de las "transversales rectas" aplicado a las medidas de ángulos en los limbos circulares o semicirculares de los instrumentos astronómicos y geográficos ha sido tratado por varios autores. Al estudiar la precisión del sistema, algunos de ellos indicaron la conveniencia de emplear "transversales circulares", en lugar de las "transversales rectas". [18]