El método de marcha de rayos es una clase de métodos de renderizado para gráficos de computadora en 3D en los que los rayos se recorren de forma iterativa, dividiendo efectivamente cada rayo en segmentos de rayos más pequeños, y muestreando alguna función en cada paso. Por ejemplo, en la proyección de rayos de volumen , la función accedería a puntos de datos de un escaneo 3D. En el trazado de esferas, la función estima una distancia para el siguiente paso. El método de marcha de rayos también se utiliza en simulaciones de física como una alternativa al trazado de rayos , donde se resuelven soluciones analíticas de las trayectorias de las ondas de luz o sonido. El método de marcha de rayos para gráficos de computadora a menudo aprovecha las SDF para determinar un tamaño de paso máximo seguro, mientras que esto es menos común en simulaciones de física, se puede lograr un método de paso adaptativo similar utilizando métodos de Runge-Kutta adaptativos .
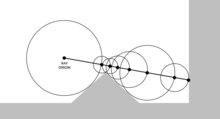
En el trazado de esferas , [1] o marcha de rayos asistida por esferas, se aproxima un punto de intersección entre el rayo y una superficie definida por una función de distancia con signo (SDF). La SDF se evalúa para cada iteración con el fin de poder dar pasos tan grandes como sea posible sin omitir ninguna parte de la superficie. Se utiliza un umbral para cancelar la iteración posterior cuando se ha alcanzado un punto que está lo suficientemente cerca de la superficie. A medida que el hardware de GPU potente se hizo más disponible, este método fue popularizado por la demoscene e Inigo Quilez, [ cita requerida ] cocreador de Shadertoy .
En el caso de escenas simples con formas 3D básicas, el ray marching no ofrece muchas ventajas con respecto al ray tracing (que encuentra intersecciones sin desplazarse por el espacio). Las ventajas del ray marching de SDF son, por ejemplo, la transformación de formas, la aproximación de sombras suaves, la repetición de geometría y las escenas definidas mediante algoritmos.
Existen funciones de distancia con signo para muchas formas 3D primitivas. [2] Se pueden combinar mediante operaciones matemáticas como módulo y booleanas para formar superficies más complejas. Por ejemplo, si se toma el módulo de las coordenadas de entrada de una función de distancia con signo, se forma un mosaico de su volumen en todo el espacio, y si se toma el máximo de dos funciones de distancia con signo, se obtiene la superficie de intersección de sus volúmenes. Debido a que las funciones de distancia con signo se pueden definir para muchos fractales, el trazado de esferas se utiliza a menudo para la representación fractal en 3D. [3]
Una técnica similar a la marcha de rayos asistida por esferas, el uso de cubos y distancia de taxi, se puede utilizar para renderizar volúmenes de vóxeles.
En la marcha de rayos volumétrica, se traza cada rayo de manera que se pueda tomar una muestra del color o la densidad a lo largo del rayo y luego combinarlos para obtener un color de píxel final. Esto se suele utilizar, por ejemplo, al renderizar nubes o exploraciones médicas en 3D.
Al representar efectos de espacio de pantalla , como el reflejo del espacio de pantalla (SSR) y las sombras del espacio de pantalla, los rayos se trazan utilizando búferes G , donde se almacenan datos de profundidad y normales de superficie para cada píxel 2D.
El artículo de 1989 "Hipertextura" [4] de Ken Perlin contiene un ejemplo temprano de un método de marcha de rayos.