Método grupal de manejo de datos

El método grupal de manejo de datos ( GMDH ) es una familia de algoritmos inductivos para el modelado matemático basado en computadora de conjuntos de datos multiparamétricos que incluye optimización estructural y paramétrica completamente automática de los modelos.

GMDH se utiliza en campos como la minería de datos , el descubrimiento de conocimiento , la predicción , el modelado de sistemas complejos , la optimización y el reconocimiento de patrones . ^[1] Los algoritmos GMDH se caracterizan por un procedimiento inductivo que realiza la clasificación de modelos polinomiales gradualmente complicados y selecciona la mejor solución por medio del criterio externo . La última sección de ^[2] contiene un resumen de las aplicaciones de GMDH en la década de 1970.

Otros nombres incluyen "red neuronal de propagación progresiva polinómica" ^[3] o "autoorganización de modelos". Fue uno de los primeros métodos de aprendizaje profundo , utilizado para entrenar una red neuronal de ocho capas en 1971. ^{[4] [5]}

Contenido matemático

Regresión polinómica

Esta sección se basa en. ^[2]

Este es el problema general del modelado estadístico de datos: considere un conjunto de datos con puntos. Cada punto contiene observaciones y un objetivo a predecir. ¿Cuál es la mejor manera de predecir el objetivo en función de las observaciones? ${\displaystyle \{(x_{1},...,x_{k};y)_{s}\}_{s=1:n}}$ ${\displaystyle n}$ ${\displaystyle x_{1},...,x_{k}}$ ${\displaystyle y}$

En primer lugar, dividimos el conjunto de datos completo en dos partes: un conjunto de entrenamiento y un conjunto de validación. El conjunto de entrenamiento se utilizaría para ajustar cada vez más parámetros del modelo, y el conjunto de validación se utilizaría para decidir qué parámetros incluir y cuándo dejar de ajustar por completo.

El GMDH comienza considerando polinomios de grado 2 en 2 variables. Supongamos que queremos predecir el objetivo utilizando solo las partes de la observación y utilizando solo polinomios de grado 2, entonces lo máximo que podemos hacer es esto: donde los parámetros se calculan mediante regresión lineal . Ahora, los parámetros dependen de lo que hayamos elegido, y no sabemos cuál deberíamos elegir, por lo que los elegimos todos. Es decir, realizamos todas esas regresiones polinómicas: obteniendo modelos polinómicos del conjunto de datos. ${\displaystyle i,j}$ $${\displaystyle y\approx f_{a,b,c,d,e,h}(x_{i},x_{j}):=a+bx_{i}+cx_{j}+dx_{i}^{2}+ex_{j}^{2}+fx_{i}x_{j}}$$ ${\displaystyle a,b,c,d,e,f}$ ${\displaystyle a,b,c,d,e,f}$ ${\displaystyle i,j}$ ${\displaystyle i,j}$ ${\displaystyle {\frac {1}{2}}k(k-1)}$ $${\displaystyle y\approx f_{(i,j);a,b,c,d,e,h}(x_{i},x_{j}):=a_{i,j}+b_{i,j}x_{i}+c_{i,j}x_{j}+d_{i,j}x_{i}^{2}+e_{i,j}x_{j}^{2}+f_{i,j}x_{i}x_{j}\quad \forall 1\leq i<j\leq k}$$ ${\displaystyle {\frac {1}{2}}k(k-1)}$

No queremos aceptar todos los modelos polinómicos, ya que contendría demasiados modelos. Para seleccionar solo el mejor subconjunto de estos modelos, ejecutamos cada modelo en el conjunto de datos de validación y seleccionamos los modelos cuyo error cuadrático medio está por debajo de un umbral. También escribimos el error cuadrático medio más pequeño obtenido como . ${\displaystyle f_{(i,j);a,b,c,d,e,h}}$ ${\displaystyle minMSE_{1}}$

Supongamos que después de este proceso hemos obtenido un conjunto de modelos. Ahora ejecutamos los modelos en el conjunto de datos de entrenamiento para obtener una secuencia de observaciones transformadas: . Ahora podemos ejecutar nuevamente el mismo algoritmo. ${\displaystyle k_{1}}$ ${\displaystyle z_{1},z_{2},...,z_{k_{1}}}$

Fig. 1. Distribución típica de errores mínimos. El proceso finaliza cuando se alcanza un mínimo.

El algoritmo continúa, dándonos . Mientras cada uno sea más pequeño que el anterior, el proceso continúa, dándonos modelos cada vez más profundos. Tan pronto como algunos , el algoritmo termina. La última capa ajustada (capa ) se descarta, ya que se ha ajustado en exceso al conjunto de entrenamiento. Se muestran las capas anteriores. ${\displaystyle minMSE_{1},minMSE_{2},...}$ ${\displaystyle minMSE}$ ${\displaystyle minMSE_{L+1}>minMSE_{L}}$ ${\displaystyle L+1}$

Existen métodos más sofisticados para decidir cuándo finalizar. Por ejemplo, se podría seguir ejecutando el algoritmo durante varios pasos más, con la esperanza de pasar un aumento temporal de . ${\displaystyle minMSE}$

En general

En lugar de un polinomio de grado 2 en 2 variables, cada unidad puede utilizar polinomios de grado superior en más variables: ^[1]

${\displaystyle Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{n}{a_{i}}x_{i}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{a_{ij}}}x_{i}x_{j}+\sum \limits _{i=1}^{n}{\sum \limits _{j=i}^{n}{\sum \limits _{k=j}^{n}{a_{ijk}}}}x_{i}x_{j}x_{k}+\cdots }$

Y de manera más general, un modelo GMDH con múltiples entradas y una salida es un subconjunto de componentes de la función base (1):

${\displaystyle Y(x_{1},\dots ,x_{n})=a_{0}+\sum \limits _{i=1}^{m}a_{i}f_{i}}$

donde f _i son funciones elementales que dependen de diferentes conjuntos de entradas, a _i son coeficientes y m es el número de componentes de la función base.

Criterios externos

Los criterios externos son objetivos de optimización del modelo, como minimizar el error cuadrático medio en el conjunto de validación, como se indicó anteriormente. Los criterios más comunes son:

• Criterio de regularidad (CR): mínimos cuadrados medios en un conjunto de validación.
• Mínimos cuadrados en un conjunto de validación cruzada .
• Criterio de sesgo mínimo o consistencia: diferencia al cuadrado entre los resultados estimados (o vectores de coeficientes) de dos modelos ajustados al conjunto A y B, dividida por las predicciones al cuadrado del conjunto B. ^[1]

Idea

Al igual que la regresión lineal, que ajusta una ecuación lineal sobre los datos, GMDH ajusta órdenes arbitrariamente altos de ecuaciones polinómicas sobre los datos. ^{[6] [7]}

Para elegir entre modelos, se utilizan dos o más subconjuntos de una muestra de datos, similar a la división entrenamiento-validación-prueba .

GMDH combinó ideas de: ^[8] modelado de caja negra , selección genética sucesiva de características por pares , ^[9] el principio de Gabor de "libertad de elección de decisiones", ^[10] y el principio de Beer de adiciones externas. ^[11]

Inspirados por una analogía entre construir un modelo a partir de datos ruidosos y enviar mensajes a través de un canal ruidoso , ^[12] propusieron un "modelado inmune al ruido": ^[6] cuanto mayor sea el ruido, menos parámetros debe tener el modelo óptimo, ya que el canal ruidoso no permite enviar más bits.

El modelo está estructurado como una red neuronal feedforward, pero sin restricciones en la profundidad, tenían un procedimiento para la generación automática de estructuras de modelos, que imita el proceso de selección biológica con características genéticas por pares.

Historia

El autor del GMDH es el científico soviético Prof. Alexey G. Ivakhnenko.

El método fue ideado en 1968 por el profesor Alexey G. Ivakhnenko en el Instituto de Cibernética de Kiev .

El período 1968-1971 se caracteriza por la aplicación de un único criterio de regularidad para la solución de los problemas de identificación, reconocimiento de patrones y previsión a corto plazo. Como funciones de referencia se utilizaron polinomios, redes lógicas, conjuntos difusos de Zadeh y fórmulas de probabilidad de Bayes. Los autores se sintieron estimulados por la altísima precisión de las previsiones con el nuevo enfoque. No se investigó la inmunidad al ruido.

Período 1972-1975 . Se resolvió el problema de modelado de datos con ruido y de información incompleta. Se propuso la selección multicriterio y la utilización de información a priori adicional para aumentar la inmunidad al ruido. Los mejores experimentos demostraron que con la definición ampliada del modelo óptimo mediante un criterio adicional, el nivel de ruido puede ser diez veces mayor que la señal. Luego se mejoró utilizando la teoría del Teorema de Shannon de la Comunicación General.

Período 1976-1979 . Se investigó la convergencia de algoritmos GMDH multicapa. Se demostró que algunos algoritmos multicapa tienen un "error de multicapa", análogo al error estático de los sistemas de control. En 1977 se propuso una solución de problemas de análisis de sistemas objetivos mediante algoritmos GMDH multicapa. Resultó que la clasificación por conjunto de criterios encuentra el único sistema óptimo de ecuaciones y, por lo tanto, muestra los elementos de un objeto complejo, sus principales variables de entrada y salida.

Período 1980-1988 . Se obtuvieron muchos resultados teóricos importantes. Se hizo evidente que los modelos físicos completos no se pueden utilizar para la previsión a largo plazo. Se demostró que los modelos no físicos de GMDH son más precisos para la aproximación y la previsión que los modelos físicos de análisis de regresión. Se desarrollaron algoritmos de dos niveles que utilizan dos escalas de tiempo diferentes para el modelado.

Desde 1989 se han desarrollado e investigado nuevos algoritmos (AC, OCC, PF) para el modelado no paramétrico de objetos difusos y SLP para sistemas expertos. ^[13] La etapa actual del desarrollo de GMDH puede describirse como el florecimiento de las redes neuronales de aprendizaje profundo y los algoritmos inductivos paralelos para computadoras multiprocesador. Dicho procedimiento se utiliza actualmente en redes de aprendizaje profundo . ^[14]

Redes neuronales de tipo GMDH

Existen muchas formas diferentes de elegir un orden para la consideración de modelos parciales. El primer orden de consideración utilizado en GMDH y originalmente llamado procedimiento inductivo multicapa es el más popular. Es una clasificación de modelos gradualmente complicados generados a partir de la función base . El mejor modelo está indicado por el mínimo de la característica del criterio externo. El procedimiento multicapa es equivalente a la red neuronal artificial con función de activación polinomial de neuronas. Por lo tanto, el algoritmo con este enfoque generalmente se conoce como red neuronal de tipo GMDH o red neuronal polinomial. Li demostró que la red neuronal de tipo GMDH funcionó mejor que los algoritmos de pronóstico clásicos como Single Exponential Smooth, Double Exponential Smooth, ARIMA y la red neuronal de retropropagación. ^[15]

GMDH combinatorio

Otro enfoque importante para la consideración de modelos parciales que se está volviendo cada vez más popular es una búsqueda combinatoria que puede ser limitada o completa. Este enfoque tiene algunas ventajas frente a las redes neuronales polinómicas, pero requiere una considerable potencia computacional y, por lo tanto, no es eficaz para objetos con una gran cantidad de entradas. Un logro importante de la GMDH combinatoria es que supera por completo el enfoque de regresión lineal si el nivel de ruido en los datos de entrada es mayor que cero. Garantiza que se encontrará el modelo más óptimo durante una clasificación exhaustiva.

El algoritmo combinatorio básico consta de los siguientes pasos:

• Divide la muestra de datos al menos en dos muestras A y B.
• Genera submuestras de A según modelos parciales con una complejidad cada vez mayor.
• Estima coeficientes de modelos parciales en cada capa de complejidad de los modelos.
• Calcula el valor del criterio externo para los modelos en la muestra B.
• Elige el mejor modelo (conjunto de modelos) indicado por el valor mínimo del criterio.
• Para el modelo seleccionado de complejidad óptima, vuelva a calcular los coeficientes en una muestra de datos completa.

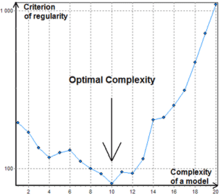
A diferencia de las redes neuronales de tipo GMDH, el algoritmo combinatorio normalmente no se detiene en un determinado nivel de complejidad porque un punto de aumento del valor del criterio puede ser simplemente un mínimo local, ver Figura 1.

Algoritmos

• Combinatoria (COMBI)
• Iterativo multicapa (MIA)
• GN
• Análisis del sistema objetivo (OSA)
• Armónico
• Dos niveles (ARIMAD)
• Multiplicativo-aditivo (MAA)
• Clusterización objetiva de computadoras (OCC);
• Algoritmo de agrupamiento de dedo señalador (PF);
• Complejación de análogos (AC)
• Rediscretización armónica
• Algoritmo basado en la Teoría Multicapa de Decisiones Estadísticas (MTSD)
• Grupo de Modelos Adaptativos de Evolución (GAME)

Implementaciones de software

• Proyecto FAKE GAME: código abierto. Multiplataforma.
• GEvom: gratuito a pedido para uso académico. Solo para Windows.
• GMDH Shell: software de análisis predictivo y pronóstico de series temporales basado en GMDH. Licencia académica gratuita y versión de prueba gratuita disponibles. Solo para Windows.
• KnowledgeMiner: producto comercial. Solo para Mac OS X. Versión de demostración gratuita disponible.
• Cliente PNN Discovery: producto comercial.
• ¡RPF científico! — Software gratuito, de código abierto.
• wGMDH: complemento de Weka , código abierto.
• Paquete R – Código abierto.
• Paquete R para tareas de regresión – Código abierto.
• Biblioteca Python del algoritmo MIA: código abierto.
• Biblioteca Python de algoritmos básicos GMDH (COMBI, MULTI, MIA, RIA) - Código abierto.

Referencias

1. Madala, HR; Ivakhnenko, OG (1994). Algoritmos de aprendizaje inductivo para el modelado de sistemas complejos. Boca Raton: CRC Press. ISBN 978-0849344381Archivado desde el original el 31 de diciembre de 2017. Consultado el 17 de noviembre de 2019 .
2. Farlow, Stanley J. (noviembre de 1981). "El algoritmo GMDH de Ivakhnenko". The American Statistician . 35 (4): 210–215. doi :10.1080/00031305.1981.10479358. ISSN  0003-1305.
3. Nikolaev, NY; Iba, H. (marzo de 2003). "Aprendizaje de redes neuronales de propagación hacia adelante polinómica mediante programación genética y retropropagación". IEEE Transactions on Neural Networks . 14 (2): 337–350. doi :10.1109/TNN.2003.809405. ISSN  1045-9227. PMID  18238017.
4. Ivakhnenko, Alexey (1971). "Teoría polinómica de sistemas complejos" (PDF) . IEEE Transactions on Systems, Man, and Cybernetics . SMC-1 (4): 364–378. doi :10.1109/TSMC.1971.4308320.
5. Schmidhuber, Jürgen (2015). "Aprendizaje profundo en redes neuronales: una descripción general". Redes neuronales . 61 : 85–117. arXiv : 1404.7828 . doi :10.1016/j.neunet.2014.09.003. PMID  25462637. S2CID  11715509.
6. Ivakhnenko, OG; Stepashko, VS (1985). Pomekhoustojchivost' Modelirovanija (Inmunidad al ruido del modelado) (PDF) . Kyiv: Naukova Dumka. Archivado desde el original (PDF) el 31 de diciembre de 2017 . Consultado el 18 de noviembre de 2019 .
7. Ivakhnenko, OG; Lapa, VG (1967). Cibernética y técnicas de pronóstico (Métodos analíticos y computacionales modernos en ciencia y matemáticas, v.8 ed.). American Elsevier.
8. Ivakhenko, AG; Savchenko, EA.; Ivakhenko, GA (octubre de 2003). "Problemas del desarrollo de futuros algoritmos GMDH". Análisis de sistemas, modelado y simulación . 43 (10): 1301–1309. doi :10.1080/0232929032000115029. ISSN  0232-9298.
9. Ivakhnenko, Aleksei G. y Grigorii A. Ivakhnenko. "Problemas de desarrollo posterior del método de grupo de algoritmos de manejo de datos. Parte I". Reconocimiento de patrones y análisis de imágenes c/c de raspoznavaniye obrazov i analiz izobrazhenii 10.2 (2000): 187-194.
10. Gabor, D. (1971). Perspectivas de la planificación. Organización para la Cooperación y el Desarrollo Económicos . Londres: Imp.Coll.
11. Beer, S. (1959). Cibernética y gestión . Londres: English Univ. Press.
12. Ivahnenko, OG (1982). Método inductivo de autoorganización de modelos para sistemas complejos (PDF) . Kiev: Naukova Dumka. Archivado desde el original (PDF) el 2017-12-31 . Consultado el 2019-11-18 .
13. Ivakhnenko, OG; Ivakhnenko, GA (1995). "Revisión de problemas solucionables mediante algoritmos del método de grupo de manejo de datos (GMDH)" (PDF) . Reconocimiento de patrones y análisis de imágenes . 5 (4): 527–535. CiteSeerX 10.1.1.19.2971 . 
14. Takao, S.; Kondo, S.; Ueno, J.; Kondo, T. (2017). "Red neuronal de tipo GMDH con retroalimentación profunda y su aplicación al análisis de imágenes médicas de imágenes cerebrales por resonancia magnética". Vida artificial y robótica . 23 (2): 161–172. doi :10.1007/s10015-017-0410-1. S2CID  44190434.
15. Li, Rita Yi Man; Fong, Simon; Chong, Kyle Weng Sang (2017). "Pronóstico de los REIT y los índices bursátiles: método de grupo de manejo de datos, enfoque de red neuronal". Revista de investigación inmobiliaria de la Cuenca del Pacífico . 23 (2): 123–160. doi :10.1080/14445921.2016.1225149. S2CID  157150897.

Lectura adicional

• AG Ivakhnenko. Autoorganización heurística en problemas de ingeniería cibernética, Automatica, vol. 6, 1970 — págs. 207-219.
• SJ Farlow . Métodos autoorganizativos en modelado: algoritmos de tipo GMDH . Nueva York, Bazel: Marcel Decker Inc., 1984, 350 págs.
• HR Madala, AG Ivakhnenko. Algoritmos de aprendizaje inductivo para el modelado de sistemas complejos. CRC Press, Boca Raton, 1994.

Enlaces externos

• Biblioteca de libros y artículos del GMDH
• Método grupal de manejo de datos