Cuenta el número de tuplas de caminos reticulares que no se intersecan
En matemáticas, el lema de Lindström-Gessel-Viennot proporciona una forma de contar la cantidad de tuplas de caminos reticulares que no se intersecan o, de manera más general, caminos en un grafo dirigido. Fue demostrado por Gessel-Viennot en 1985, basándose en un trabajo previo de Lindström publicado en 1973.
Declaración
Sea G un grafo acíclico dirigido localmente finito . Esto significa que cada vértice tiene grado finito y que G no contiene ciclos dirigidos. Considere los vértices base y los vértices de destino , y asigne también un peso a cada arista dirigida e . Se supone que estos pesos de arista pertenecen a algún anillo conmutativo . Para cada camino dirigido P entre dos vértices, sea el producto de los pesos de las aristas del camino. Para dos vértices cualesquiera a y b , escriba e ( a , b ) para la suma de todos los caminos de a a b . Esto está bien definido si entre dos puntos cualesquiera hay solo un número finito de caminos; pero incluso en el caso general, esto puede estar bien definido bajo algunas circunstancias (como que todos los pesos de arista sean indeterminados formales distintos por pares y se consideren como una serie de potencias formales ). Si uno asigna el peso 1 a cada arista, entonces e ( a , b ) cuenta el número de caminos de a a b .





Con esta configuración, escribe
 .
.
Una n -tupla de caminos que no se intersecan de A a B significa una n -tupla ( P 1 , ..., P n ) de caminos en G con las siguientes propiedades:
- Existe una permutación de tal que, para cada i , el camino P i es un camino de a .




- Siempre que , los caminos P i y P j no tienen dos vértices en común (ni siquiera puntos finales).

Dada tal n- tupla ( P 1 , ..., P n ), denotamos por la permutación de de la primera condición.

El lema de Lindström–Gessel–Viennot establece entonces que el determinante de M es la suma con signo de todas las n -tuplas P = ( P 1 , ..., P n ) de caminos no intersecantes de A a B :

Es decir, el determinante de M cuenta los pesos de todas las n -tuplas de caminos no intersecantes que comienzan en A y terminan en B , cada uno afectado con el signo de la permutación correspondiente de , dada al tomar como .



En particular, si la única permutación posible es la identidad (es decir, cada n -tupla de caminos que no se intersecan de A a B toma a i a b i para cada i ) y tomamos los pesos como 1, entonces det( M ) es exactamente el número de n -tuplas que no se intersecan de caminos que comienzan en A y terminan en B .
Prueba
Para demostrar el lema de Lindström–Gessel–Viennot, primero introducimos algo de notación.
Un n -camino desde una n -tupla de vértices de G a una n -tupla de vértices de G significará una n -tupla de caminos en G , y cada uno de ellos conduce desde a . Este n -camino se llamará no intersecante solo en caso de que los caminos P i y P j no tengan dos vértices en común (incluidos los puntos finales) siempre que . De lo contrario, se llamará entrelazado .






Dada una ruta n , el peso de esta ruta n se define como el producto .


Un n -camino torcido desde una n -tupla de vértices de G hasta una n -tupla de vértices de G significará un n -camino desde a para alguna permutación en el grupo simétrico . Esta permutación se llamará el giro de este n -camino torcido, y se denotará por (donde P es el n -camino). Esto, por supuesto, generaliza la notación introducida anteriormente.








Recordando la definición de M , podemos expandir det M como una suma con signo de permutaciones; así obtenemos

Queda por demostrar que la suma de todos los n -caminos entrelazados y retorcidos se anula. Sea n el conjunto de n- caminos entrelazados y retorcidos . Para establecer esto, construiremos una involución con las propiedades y para todo . Dada tal involución, el resto del término






en la suma anterior se reduce a 0, ya que sus sumandos se cancelan entre sí (es decir, el sumando correspondiente a cada uno cancela el sumando correspondiente a ).

Construcción de la involución: La idea detrás de la definición de la involución es elegir dos caminos que se intersectan dentro de un camino entrelazado, e intercambiar sus colas después de su punto de intersección. En general, hay varios pares de caminos que se intersectan, que también pueden intersecarse varias veces; por lo tanto, se debe hacer una elección cuidadosa. Sea cualquier camino entrelazado torcido n . Entonces se define de la siguiente manera. Llamamos a un vértice abarrotado si pertenece al menos a dos de los caminos . El hecho de que el grafo sea acíclico implica que esto es equivalente a "aparecer al menos dos veces en todos los caminos". [1] Como P está entrelazado, hay al menos un vértice abarrotado. Escogemos el más pequeño tal que contiene un vértice abarrotado. Luego, escogemos el primer vértice abarrotado v en ("primero" en el sentido de "encontrado primero al viajar a lo largo de "), y escogemos el j más grande tal que v pertenece a . El abarrotamiento de v implica j > i . Escribimos los dos caminos y como











donde , y donde y se eligen de manera que v sea el -ésimo vértice a lo largo de y el -ésimo vértice a lo largo de (es decir, ). Establecemos y y y . Ahora definamos la ruta n torcida para que coincida con excepto para los componentes y , que se reemplazan por
















Es evidente de inmediato que es un camino n entrelazado y retorcido . Al seguir los pasos de la construcción, es fácil ver que , y además que y , de modo que aplicar de nuevo a implica intercambiar las colas de y dejar los otros componentes intactos. Por lo tanto . Por lo tanto, es una involución. Queda por demostrar las propiedades de antisimetría deseadas:









De la construcción se puede ver que coincide con excepto que intercambia y , por lo que da como resultado . Para demostrar que primero calculamos, apelando al intercambio de cola






Por eso .
De esta forma hemos encontrado una involución con las propiedades deseadas y hemos completado la prueba del lema de Lindström-Gessel-Viennot.
Observación. Argumentos similares al anterior aparecen en varias fuentes, con variaciones en cuanto a la elección de qué colas cambiar. Una versión con j más pequeño (desigual a i ) en lugar de más grande aparece en la referencia de Gessel-Viennot 1989 (prueba del Teorema 1).
Aplicaciones
Polinomios de Schur
El lema de Lindström–Gessel–Viennot se puede utilizar para demostrar la equivalencia de las siguientes dos definiciones diferentes de polinomios de Schur . Dada una partición de n , el polinomio de Schur se puede definir como:


donde la suma es sobre todas las tablas de Young semiestándar T de forma λ , y el peso de una tabla T se define como el monomio obtenido al tomar el producto de las x i indexadas por las entradas i de T . Por ejemplo, el peso de la tabla es .
es .

donde h i son los polinomios simétricos homogéneos completos ( entendiéndose h i como 0 si i es negativo). Por ejemplo, para la partición (3,2,2,1), el determinante correspondiente es

Para probar la equivalencia, dada cualquier partición λ como la anterior, se consideran los r puntos iniciales y los r puntos finales como puntos en la red , que adquiere la estructura de un grafo dirigido al afirmar que las únicas direcciones permitidas son ir uno a la derecha o uno hacia arriba; el peso asociado a cualquier borde horizontal a la altura i es x i , y el peso asociado a un borde vertical es 1. Con esta definición, las r -tuplas de caminos de A a B son exactamente tablas de Young semiestándar de forma λ , y el peso de dicha r -tupla es el sumando correspondiente en la primera definición de los polinomios de Schur. Por ejemplo, con la tabla


 , se obtiene la 4 -tupla correspondiente
, se obtiene la 4 -tupla correspondiente

Por otra parte, la matriz M es exactamente la matriz escrita anteriormente para D. Esto muestra la equivalencia requerida. (Véase también §4.5 en el libro de Sagan, o la Primera demostración del teorema 7.16.1 en el EC2 de Stanley, o §3.3 en la preimpresión de Fulmek en arXiv, o §9.13 en las notas de la clase de Martin, para ligeras variaciones de este argumento.)
La fórmula de Cauchy-Binet
También se puede utilizar el lema de Lindström–Gessel–Viennot para demostrar la fórmula de Cauchy–Binet y, en particular, la multiplicidad del determinante.
Generalizaciones
La fórmula de Talaska
La aciclicidad de G es un supuesto esencial del lema de Lindström–Gessel–Viennot; garantiza (en situaciones razonables) que las sumas estén bien definidas y se incorpora a la prueba (si G no es acíclica, entonces f podría transformar una autointersección de un camino en una intersección de dos caminos distintos, lo que rompe el argumento de que f es una involución). Sin embargo, el artículo de Kelli Talaska de 2012 establece una fórmula que generaliza el lema a dígrafos arbitrarios. Las sumas se reemplazan por series de potencias formales y la suma sobre tuplas de caminos que no se intersecan ahora se convierte en una suma sobre colecciones de caminos y ciclos que no se intersecan y que no se autointersecan, dividida por una suma sobre colecciones de ciclos que no se intersecan. Se remite al lector al artículo de Talaska para obtener más detalles.

Véase también
Referencias
- ^ Si el gráfico no fuera acíclico, el "hacinamiento" podría cambiar después de aplicar ; esta prueba no funcionaría y el lema en realidad se volvería totalmente falso.

- Gessel, Ira M. ; Viennot, Xavier G. (1989), Determinantes, caminos y particiones de planos (PDF) , archivado desde el original (PDF) el 17 de abril de 2017
- Lindström, Bernt (1973), Sobre las representaciones vectoriales de matroides inducidos , doi :10.1112/blms/5.1.8 (inactivo 2024-10-17)
{{citation}}: CS1 maint: DOI inactive as of October 2024 (link) - Sagan, Bruce E. (2001), El grupo simétrico , Springer
- Stanley, Richard P. (1999), Combinatoria enumerativa, volumen 2 , CUP
- Talaska, Kelli (2012), Determinantes de matrices de rutas ponderadas , arXiv : 1202.3128v1
- Martin, Jeremy (2012), Apuntes de clase sobre combinatoria algebraica (PDF)
- Fulmek, Markus (2010), Ver los determinantes como caminos reticulares que no se intersecan produce identidades determinantes clásicas de manera biyectiva , arXiv : 1010.3860v1
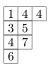 es .
es . , se obtiene la 4 -tupla correspondiente
, se obtiene la 4 -tupla correspondiente