Algoritmo de ocho puntos

El algoritmo de ocho puntos es un algoritmo utilizado en visión artificial para estimar la matriz esencial o la matriz fundamental relacionada con un par de cámaras estéreo a partir de un conjunto de puntos de imagen correspondientes. Fue introducido por Christopher Longuet-Higgins en 1981 para el caso de la matriz esencial. En teoría, este algoritmo también se puede utilizar para la matriz fundamental, pero en la práctica el algoritmo normalizado de ocho puntos, descrito por Richard Hartley en 1997, es más adecuado para este caso.

El nombre del algoritmo se debe a que estima la matriz esencial o matriz fundamental a partir de un conjunto de ocho (o más) puntos de imagen correspondientes. Sin embargo, se pueden utilizar variaciones del algoritmo para menos de ocho puntos.

Restricción de coplanaridad

Ejemplo de geometría epipolar. Dos cámaras, con sus respectivos centros de proyección O _L y O _R , observan un punto P . La proyección de P sobre cada uno de los planos de la imagen se denota p _L y p _R . Los puntos E _L y E _R son los epipolos.

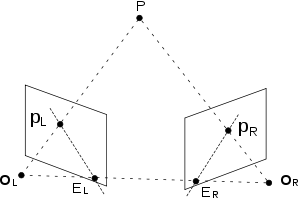
Se puede expresar la geometría epipolar de dos cámaras y un punto en el espacio con una ecuación algebraica. Observe que, sin importar dónde se encuentre el punto en el espacio, los vectores , y pertenecen al mismo plano. Llamemos a las coordenadas del punto en el marco de referencia del ojo izquierdo y a las coordenadas de en el marco de referencia del ojo derecho y a la rotación y traslación entre los dos marcos de referencia st es la relación entre las coordenadas de en los dos marcos de referencia. La siguiente ecuación siempre se cumple porque el vector generado a partir de es ortogonal a ambos y  : ${\displaystyle P}$ ${\displaystyle {\overline {O_{L}P}}}$ ${\displaystyle {\overline {O_{R}P}}}$ ${\displaystyle {\overline {O_{R}O_{L}}}}$ ${\displaystyle X_{L}}$ ${\displaystyle P}$ ${\displaystyle X_{R}}$ ${\displaystyle P}$ ${\displaystyle R,T}$ ${\displaystyle X_{R}=R(X_{L}-T)}$ ${\displaystyle P}$ ${\displaystyle T\wedge X_{L}}$ ${\displaystyle T}$ ${\displaystyle X_{L}}$

${\displaystyle X_{L}^{T}T\wedge X_{L}-T^{T}T\wedge X_{L}=(X_{L}-T)^{T}T\wedge X_{L}=0}$

Porque , obtenemos ${\displaystyle I=R^{T}R}$

${\displaystyle (X_{L}-T)^{T}R^{T}RT\wedge X_{L}=0}$.

Reemplazando por , obtenemos ${\displaystyle (X_{L}-T)^{T}R^{T}}$ ${\displaystyle X_{R}^{T}}$

${\displaystyle X_{R}^{T}RT\wedge X_{L}=X_{R}^{T}RSX_{L}=X_{R}^{T}EX_{L}=0}$

Observe que puede considerarse como una matriz; Longuet-Higgins utilizó el símbolo para denotarlo. El producto a menudo se denomina matriz esencial y se denota con . ${\displaystyle T\wedge }$ ${\displaystyle S}$ ${\displaystyle RT\wedge =RS}$ ${\displaystyle E}$

Los vectores son paralelos a los vectores y, por lo tanto, la restricción de coplanaridad se cumple si sustituimos estos vectores. Si llamamos a las coordenadas de las proyecciones de sobre los planos de imagen izquierdo y derecho, entonces la restricción de coplanaridad puede escribirse como ${\displaystyle {\overline {O_{L}p_{L}}},{\overline {O_{R}p_{R}}}}$ ${\displaystyle {\overline {O_{L}P}},{\overline {O_{R}P}}}$ ${\displaystyle y,y'}$ ${\displaystyle P}$

${\displaystyle y'^{T}\mathbf {E} y=0}$

Algoritmo básico

El algoritmo básico de ocho puntos se describe aquí para el caso de la estimación de la matriz esencial . Consta de tres pasos. Primero, formula una ecuación lineal homogénea , donde la solución está directamente relacionada con , y luego resuelve la ecuación, teniendo en cuenta que puede no tener una solución exacta. Finalmente, se gestionan las restricciones internas de la matriz resultante. El primer paso se describe en el artículo de Longuet-Higgins, el segundo y el tercer paso son enfoques estándar en la teoría de la estimación. ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {E} }$

La restricción definida por la matriz esencial es ${\displaystyle \mathbf {E} }$

${\displaystyle (\mathbf {y} ')^{T}\,\mathbf {E} \,\mathbf {y} =0}$

para los puntos de imagen correspondientes representados en coordenadas de imagen normalizadas . El problema que resuelve el algoritmo es determinar para un conjunto de puntos de imagen coincidentes. En la práctica, las coordenadas de imagen de los puntos de imagen se ven afectadas por el ruido y la solución también puede estar sobredeterminada, lo que significa que puede no ser posible encontrar la que satisface la restricción anterior exactamente para todos los puntos. Esta cuestión se aborda en el segundo paso del algoritmo. ${\displaystyle \mathbf {y} ,\mathbf {y} '}$ ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {E} }$

Paso 1: Formulación de unaecuación lineal homogénea

Con

${\displaystyle \mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\1\end{pmatrix}}}$   y     y   ${\displaystyle \mathbf {y} '={\begin{pmatrix}y'_{1}\\y'_{2}\\1\end{pmatrix}}}$ ${\displaystyle \mathbf {E} ={\begin{pmatrix}e_{11}&e_{12}&e_{13}\\e_{21}&e_{22}&e_{23}\\e_{31}&e_{32}&e_{33}\end{pmatrix}}}$

La restricción también se puede reescribir como

${\displaystyle y'_{1}y_{1}e_{11}+y'_{1}y_{2}e_{12}+y'_{1}e_{13}+y'_{2}y_{1}e_{21}+y'_{2}y_{2}e_{22}+y'_{2}e_{23}+y_{1}e_{31}+y_{2}e_{32}+e_{33}=0\,}$

o

${\displaystyle \mathbf {e} \cdot {\tilde {\mathbf {y} }}=0}$

dónde

${\displaystyle {\tilde {\mathbf {y} }}={\begin{pmatrix}y'_{1}y_{1}\\y'_{1}y_{2}\\y'_{1}\\y'_{2}y_{1}\\y'_{2}y_{2}\\y'_{2}\\y_{1}\\y_{2}\\1\end{pmatrix}}}$   y   ${\displaystyle \mathbf {e} ={\begin{pmatrix}e_{11}\\e_{12}\\e_{13}\\e_{21}\\e_{22}\\e_{23}\\e_{31}\\e_{32}\\e_{33}\end{pmatrix}}}$

es decir, representa la matriz esencial en forma de un vector de 9 dimensiones y este vector debe ser ortogonal al vector que puede verse como una representación vectorial de la matriz . ${\displaystyle \mathbf {e} }$ ${\displaystyle {\tilde {\mathbf {y} }}}$ ${\displaystyle 3\times 3}$ ${\displaystyle \mathbf {y} '\,\mathbf {y} ^{T}}$

Cada par de puntos de imagen correspondientes produce un vector . Dado un conjunto de puntos 3D, esto corresponde a un conjunto de vectores y todos ellos deben satisfacer ${\displaystyle {\tilde {\mathbf {y} }}}$ ${\displaystyle \mathbf {P} _{k}}$ ${\displaystyle {\tilde {\mathbf {y} }}_{k}}$

${\displaystyle \mathbf {e} \cdot {\tilde {\mathbf {y} }}_{k}=0}$

para el vector . Dados suficientes vectores linealmente independientes (al menos ocho), es posible determinar de manera sencilla. Reúna todos los vectores como columnas de una matriz y entonces debe darse el caso de que ${\displaystyle \mathbf {e} }$ ${\displaystyle {\tilde {\mathbf {y} }}_{k}}$ ${\displaystyle \mathbf {e} }$ ${\displaystyle {\tilde {\mathbf {y} }}_{k}}$ ${\displaystyle \mathbf {Y} }$

${\displaystyle \mathbf {e} ^{T}\,\mathbf {Y} =\mathbf {0} }$

Esto significa que es la solución de una ecuación lineal homogénea . ${\displaystyle \mathbf {e} }$

Paso 2: Resolver la ecuación

Un enfoque estándar para resolver esta ecuación implica que es un vector singular derecho de correspondiente a un valor singular que es igual a cero. Siempre que se utilicen al menos ocho vectores linealmente independientes para construir , se deduce que este vector singular es único (sin tener en cuenta la multiplicación escalar) y, en consecuencia, y puede determinarse. ${\displaystyle \mathbf {e} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle {\tilde {\mathbf {y} }}_{k}}$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {e} }$ ${\displaystyle \mathbf {E} }$

En el caso de que se utilicen más de ocho puntos correspondientes para construir, es posible que no tenga ningún valor singular igual a cero. Este caso se da en la práctica cuando las coordenadas de la imagen se ven afectadas por varios tipos de ruido. Un enfoque común para tratar esta situación es describirla como un problema de mínimos cuadrados totales ; encontrar cuál minimiza ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {e} }$

${\displaystyle \|\mathbf {e} ^{T}\,\mathbf {Y} \|}$

cuando . La solución es elegir como el vector singular izquierdo correspondiente al valor singular más pequeño de . Una reordenación de esto nuevamente en una matriz da el resultado de este paso, aquí denominado . ${\displaystyle \|\mathbf {e} \|=1}$ ${\displaystyle \mathbf {e} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {e} }$ ${\displaystyle 3\times 3}$ ${\displaystyle \mathbf {E} _{\rm {est}}}$

Paso 3: Aplicación de la restricción interna

Otra consecuencia de trabajar con coordenadas de imagen ruidosas es que la matriz resultante puede no satisfacer la restricción interna de la matriz esencial, es decir, dos de sus valores singulares son iguales y distintos de cero y el otro es cero. Dependiendo de la aplicación, las desviaciones más pequeñas o más grandes de la restricción interna pueden o no ser un problema. Si es crítico que la matriz estimada satisfaga las restricciones internas, esto se puede lograr encontrando la matriz de rango 2 que minimice ${\displaystyle \mathbf {E} '}$

${\displaystyle \|\mathbf {E} '-\mathbf {E} _{\rm {est}}\|}$

donde es la matriz resultante del Paso 2 y se utiliza la norma matricial de Frobenius . La solución del problema se obtiene calculando primero una descomposición en valores singulares de : ${\displaystyle \mathbf {E} _{\rm {est}}}$ ${\displaystyle \mathbf {E} _{\rm {est}}}$

${\displaystyle \mathbf {E} _{\rm {est}}=\mathbf {U} \,\mathbf {S} \,\mathbf {V} ^{T}}$

donde son matrices ortogonales y es una matriz diagonal que contiene los valores singulares de . En el caso ideal, uno de los elementos diagonales de debería ser cero, o al menos pequeño en comparación con los otros dos que deberían ser iguales. En cualquier caso, establezca ${\displaystyle \mathbf {U} ,\mathbf {V} }$ ${\displaystyle \mathbf {S} }$ ${\displaystyle \mathbf {E} _{\rm {est}}}$ ${\displaystyle \mathbf {S} }$

${\displaystyle \mathbf {S} '={\begin{pmatrix}s_{1}&0&0\\0&s_{2}&0\\0&0&0\end{pmatrix}},}$

donde son los valores singulares más grande y segundo más grande respectivamente. Finalmente, se da por ${\displaystyle s_{1},s_{2}}$ ${\displaystyle \mathbf {S} }$ ${\displaystyle \mathbf {E} '}$

${\displaystyle \mathbf {E} '=\mathbf {U} \,\mathbf {S} '\,\mathbf {V} ^{T}}$

La matriz es la estimación resultante de la matriz esencial proporcionada por el algoritmo. ${\displaystyle \mathbf {E} '}$

Algoritmo normalizado

El algoritmo básico de ocho puntos se puede utilizar también, en principio, para estimar la matriz fundamental . La restricción definitoria para es ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {F} }$

${\displaystyle (\mathbf {y} ')^{T}\,\mathbf {F} \,\mathbf {y} =0}$

donde son las representaciones homogéneas de las coordenadas de la imagen correspondiente (no necesariamente normalizadas). Esto significa que es posible formar una matriz de manera similar a la matriz esencial y resolver la ecuación ${\displaystyle \mathbf {y} ,\mathbf {y} '}$ ${\displaystyle \mathbf {Y} }$

${\displaystyle \mathbf {f} ^{T}\,\mathbf {Y} =\mathbf {0} }$

para el cual es una versión reformada de . Siguiendo el procedimiento descrito anteriormente, es posible determinar a partir de un conjunto de ocho puntos coincidentes. En la práctica, sin embargo, la matriz fundamental resultante puede no ser útil para determinar las restricciones epipolares. ${\displaystyle \mathbf {f} }$ ${\displaystyle \mathbf {F} }$ ${\displaystyle \mathbf {F} }$

Dificultad

El problema es que el resultado a menudo está mal condicionado . En teoría, debería tener un valor singular igual a cero y el resto son distintos de cero. En la práctica, sin embargo, algunos de los valores singulares distintos de cero pueden resultar pequeños en relación con los mayores. Si se utilizan más de ocho puntos correspondientes para construir , donde las coordenadas son solo aproximadamente correctas, puede que no haya un valor singular bien definido que pueda identificarse como aproximadamente cero. En consecuencia, la solución del sistema de ecuaciones lineal homogéneo puede no ser lo suficientemente precisa como para ser útil. ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {Y} }$

Causa

Hartley abordó este problema de estimación en su artículo de 1997. Su análisis del problema muestra que el problema se debe a la mala distribución de las coordenadas de la imagen homogénea en su espacio, . Una representación homogénea típica de la coordenada de la imagen 2D es ${\displaystyle \mathbb {R} ^{3}}$ ${\displaystyle (y_{1},y_{2})\,}$

${\displaystyle \mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\1\end{pmatrix}}}$

donde ambos se encuentran en el rango de 0 a 1000–2000 para una cámara digital moderna. Esto significa que las dos primeras coordenadas en varían en un rango mucho mayor que la tercera coordenada. Además, si los puntos de la imagen que se utilizan para construir se encuentran en una región relativamente pequeña de la imagen, por ejemplo en , nuevamente el vector apunta más o menos en la misma dirección para todos los puntos. Como consecuencia, tendrá un valor singular grande y los restantes son pequeños. ${\displaystyle y_{1},y_{2}\,}$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle (700,700)\pm (100,100)\,}$ ${\displaystyle \mathbf {y} }$ ${\displaystyle \mathbf {Y} }$

Solución

Como solución a este problema, Hartley propuso que el sistema de coordenadas de cada una de las dos imágenes se transformara, independientemente, en un nuevo sistema de coordenadas según el siguiente principio.

• El origen del nuevo sistema de coordenadas debe estar centrado (tener su origen) en el centroide (centro de gravedad) de los puntos de la imagen. Esto se logra mediante una traslación del origen original al nuevo.
• Después de la traducción, las coordenadas se escalan uniformemente de modo que la media de las distancias desde el origen hasta los puntos sea igual a . ${\displaystyle {\sqrt {2}}}$

Este principio da como resultado, normalmente, una transformación de coordenadas distinta para cada una de las dos imágenes. Como resultado, las nuevas coordenadas de la imagen homogénea vienen dadas por ${\displaystyle \mathbf {\bar {y}} ,\mathbf {\bar {y}} '}$

${\displaystyle \mathbf {\bar {y}} =\mathbf {T} \,\mathbf {y} }$

${\displaystyle \mathbf {\bar {y}} '=\mathbf {T} '\,\mathbf {y} '}$

donde se encuentran las transformaciones (traslación y escala) de las coordenadas de imagen normalizadas antiguas a las nuevas . Esta normalización depende únicamente de los puntos de imagen que se utilizan en una sola imagen y, en general, es distinta de las coordenadas de imagen normalizadas producidas por una cámara normalizada. ${\displaystyle \mathbf {T} ,\mathbf {T} '}$

La restricción epipolar basada en la matriz fundamental ahora se puede reescribir como

${\displaystyle 0=(\mathbf {\bar {y}} ')^{T}\,((\mathbf {T} ')^{T})^{-1}\,\mathbf {F} \,\mathbf {T} ^{-1}\,\mathbf {\bar {y}} =(\mathbf {\bar {y}} ')^{T}\,\mathbf {\bar {F}} \,\mathbf {\bar {y}} }$

donde . Esto significa que es posible utilizar las coordenadas de la imagen homogénea normalizada para estimar la matriz fundamental transformada utilizando el algoritmo básico de ocho puntos descrito anteriormente. ${\displaystyle \mathbf {\bar {F}} =((\mathbf {T} ')^{T})^{-1}\,\mathbf {F} \,\mathbf {T} ^{-1}}$ ${\displaystyle \mathbf {\bar {y}} ,\mathbf {\bar {y}} '}$ ${\displaystyle \mathbf {\bar {F}} }$

El propósito de las transformaciones de normalización es que la matriz , construida a partir de las coordenadas de la imagen normalizada, en general, tenga un número de condición mejor que tiene. Esto significa que la solución está mejor definida como una solución de la ecuación homogénea que en relación con . Una vez que se ha determinado y se ha reformado en esta última, se puede desnormalizar para dar de acuerdo con ${\displaystyle \mathbf {\bar {Y}} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {\bar {f}} }$ ${\displaystyle \mathbf {\bar {Y}} \,\mathbf {\bar {f}} }$ ${\displaystyle \mathbf {f} }$ ${\displaystyle \mathbf {Y} }$ ${\displaystyle \mathbf {\bar {f}} }$ ${\displaystyle \mathbf {\bar {F}} }$ ${\displaystyle \mathbf {F} }$

${\displaystyle \mathbf {F} =(\mathbf {T} ')^{T}\,\mathbf {\bar {F}} \,\mathbf {T} }$

En general, esta estimación de la matriz fundamental es mejor que la que se habría obtenido estimándola a partir de las coordenadas no normalizadas.

Utilizando menos de ocho puntos

Cada par de puntos contribuye con una ecuación restrictiva sobre el elemento en . Dado que tiene cinco grados de libertad, debería ser suficiente con solo cinco pares de puntos para determinar . David Nister propuso una solución eficiente para estimar la matriz esencial a partir de un conjunto de cinco puntos pareados, conocido como el algoritmo de cinco puntos. ^[1] Hartley et. al. propusieron posteriormente un algoritmo de cinco puntos modificado y más estable basado en el algoritmo de Nister. ^[2] ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {E} }$ ${\displaystyle \mathbf {E} }$

Véase también

• Matriz esencial
  • Matriz esencial § Extracción de rotación y traslación
• Matriz fundamental
• Tensor trifocal

Referencias

1. Nister, David (2004). "Una solución eficiente al problema de la pose relativa de cinco puntos". IEEE Transactions on Pattern Analysis and Machine Intelligence . 26 (6): 756–770. doi :10.1109/TPAMI.2004.17. PMID  18579936. S2CID  886598.
2. Li, Hongdong (2006). "Estimación de movimiento de cinco puntos simplificada". 18.ª Conferencia internacional sobre reconocimiento de patrones (ICPR'06) . pp. 630–633. doi :10.1109/ICPR.2006.579. ISBN 0-7695-2521-0.S2CID 7745676  .

Lectura adicional

• Richard I. Hartley (junio de 1997). "En defensa del algoritmo de ocho puntos". IEEE Transactions on Pattern Analysis and Machine Intelligence . 19 (6): 580–593. doi :10.1109/34.601246. S2CID  16919747.

• Richard Hartley y Andrew Zisserman (2003). Geometría de vista múltiple en visión artificial . Cambridge University Press. ISBN 978-0-521-54051-3.

• H. Christopher Longuet-Higgins (septiembre de 1981). "Un algoritmo informático para reconstruir una escena a partir de dos proyecciones". Nature . 293 (5828): 133–135. Bibcode :1981Natur.293..133L. doi :10.1038/293133a0. S2CID  4327732.