Muchos sistemas de tipos de lenguajes de programación admiten la subtipificación . Por ejemplo, si el tipo es un subtipo de , entonces una expresión de tipo debería poder sustituirse dondequiera que se utilice una expresión de tipo . CatAnimalCat Animal
La varianza es la relación entre la subtipificación entre tipos más complejos y la subtipificación entre sus componentes. Por ejemplo, ¿cómo debería relacionarse una lista de Cats con una lista de Animals? ¿O cómo debería relacionarse una función que devuelve s Cat con una función que devuelve Animal?
Según la varianza del constructor de tipo , la relación de subtipo de los tipos simples puede conservarse, invertirse o ignorarse para los respectivos tipos complejos. En el lenguaje de programación OCaml , por ejemplo, "lista de Gato" es un subtipo de "lista de Animal" porque el constructor de tipo de lista es covariante . Esto significa que la relación de subtipo de los tipos simples se conserva para los tipos complejos.
Por otra parte, "función de Animal a String" es un subtipo de "función de Cat a String" porque el constructor del tipo de función es contravariante en el tipo de parámetro . Aquí, la relación de subtipos de los tipos simples se invierte para los tipos complejos.
Un diseñador de lenguaje de programación tendrá en cuenta la varianza al idear reglas de tipado para características del lenguaje como matrices , herencia y tipos de datos genéricos . Al hacer que los constructores de tipos sean covariantes o contravariantes en lugar de invariantes , se aceptarán más programas como bien tipados. Por otro lado, los programadores a menudo encuentran que la contravarianza es poco intuitiva, y el seguimiento preciso de la varianza para evitar errores de tipo en tiempo de ejecución puede conducir a reglas de tipado complejas.
Para mantener el sistema de tipos simple y permitir programas útiles, un lenguaje puede tratar a un constructor de tipos como invariante incluso si sería seguro considerarlo variante, o tratarlo como covariante incluso si eso pudiera violar la seguridad de tipos.
Supongamos Aque y Bson tipos, y I<U>denota la aplicación de un constructor de tipo I con argumento de tipo U. Dentro del sistema de tipos de un lenguaje de programación, una regla de tipado para un constructor de tipo Ies:
A ≤ B, entonces I<A> ≤ I<B>;A ≤ B, entonces I<B> ≤ I<A>;A ≤ B, entonces I<A> ≡ I<B>); [1]El artículo analiza cómo se aplica esto a algunos constructores de tipos comunes.
Por ejemplo, en C# , si Cates un subtipo de Animal, entonces:
IEnumerable<Cat>es un subtipo de . El subtipo se conserva porque es covariante en .IEnumerable<Animal>IEnumerable<T>TAction<Animal>es un subtipo de . La subtipificación se invierte porque es contravariante en .Action<Cat>Action<T>TIList<Cat>IList<Animal>IList<T>TLa varianza de una interfaz genérica de C# se declara colocando el atributo out(covariante) o in(contravariante) en (cero o más de) sus parámetros de tipo. [2] : 144 Las interfaces anteriores se declaran como , , y . Los tipos con más de un parámetro de tipo pueden especificar diferentes varianzas en cada parámetro de tipo. Por ejemplo, el tipo delegado representa una función con un parámetro de entrada contravariante de tipo y un valor de retorno covariante de tipo . [3] [2] : 145 El compilador verifica que todos los tipos estén definidos y utilizados de manera consistente con sus anotaciones y, de lo contrario, señala un error de compilación.IEnumerable<out T>Action<in T>IList<T>Func<in T, out TResult>TTResult
Las reglas de tipado para la varianza de la interfaz garantizan la seguridad de los tipos. Por ejemplo, an representa una función de primera clase que espera un argumento de tipo , [2] : 144 y siempre se puede usar una función que pueda manejar cualquier tipo de animal en lugar de una que solo pueda manejar gatos.Action<T>T
Los tipos de datos de solo lectura (fuentes) pueden ser covariantes; los tipos de datos de solo escritura (receptores) pueden ser contravariantes. Los tipos de datos mutables que actúan como fuentes y receptores deben ser invariantes. Para ilustrar este fenómeno general, considere el tipo de matriz . Para el tipo Animalpodemos crear el tipo , que es una "matriz de animales". Para los fines de este ejemplo, esta matriz admite elementos de lectura y escritura.Animal[]
Tenemos la opción de tratar esto como:
Cat[]Animal[]Animal[]Cat[]Animal[]Cat[]Cat[]Animal[]Si deseamos evitar errores de tipo, entonces solo la tercera opción es segura. Claramente, no se puede tratar a every como si fuera a , ya que un cliente que lee desde la matriz esperará a , pero an puede contener, por ejemplo, a . Por lo tanto, la regla contravariante no es segura.Animal[]Cat[]CatAnimal[]Dog
Por el contrario, a no puede tratarse como un . Siempre debería ser posible poner a en un . Con arreglos covariantes, no se puede garantizar que esto sea seguro, ya que el almacenamiento de respaldo podría ser en realidad un arreglo de gatos. Por lo tanto, la regla covariante tampoco es segura: el constructor del arreglo debería ser invariante . Tenga en cuenta que esto solo es un problema para arreglos mutables; la regla covariante es segura para arreglos inmutables (de solo lectura). Del mismo modo, la regla contravariante sería segura para arreglos de solo escritura.Cat[]Animal[]DogAnimal[]
Las primeras versiones de Java y C# no incluían genéricos, también denominados polimorfismo paramétrico . En ese contexto, hacer que las matrices sean invariantes descarta programas polimórficos útiles.
Por ejemplo, considere escribir una función para mezclar una matriz, o una función que pruebe la igualdad de dos matrices utilizando el método Object. equalsen los elementos. La implementación no depende del tipo exacto de elemento almacenado en la matriz, por lo que debería ser posible escribir una única función que funcione en todos los tipos de matrices. Es fácil implementar funciones del tipo:
booleano equalArrays ( Objeto [] a1 , Objeto [] a2 ); void shuffleArray ( Objeto [] a ); Sin embargo, si los tipos de matriz se trataran como invariantes, solo sería posible llamar a estas funciones en una matriz de exactamente el tipo . No se podría, por ejemplo, mezclar una matriz de cadenas.Object[]
Por lo tanto, tanto Java como C# tratan los tipos de matriz de forma covariante. Por ejemplo, en Java es un subtipo de y en C# es un subtipo de .String[]Object[]string[]object[]
Como se mencionó anteriormente, las matrices covariantes generan problemas con las escrituras en la matriz. Java [4] : 126 y C# se ocupan de esto marcando cada objeto de matriz con un tipo cuando se crea. Cada vez que se almacena un valor en una matriz, el entorno de ejecución verificará que el tipo de tiempo de ejecución del valor sea igual al tipo de tiempo de ejecución de la matriz. Si hay una discrepancia, se lanza un error ArrayStoreException(Java) [4] : 126 o ArrayTypeMismatchException(C#):
// a es una matriz de un solo elemento de String String [] a = new String [ 1 ] ; // b es una matriz de Objeto Objeto [] b = a ; // Asignar un entero a b. Esto sería posible si b realmente fuera // una matriz de objetos, pero como en realidad es una matriz de cadenas, // obtendremos una java.lang.ArrayStoreException. b [ 0 ] = 1 ; En el ejemplo anterior, se puede leer de la matriz (b) de forma segura. Lo único que puede causar problemas es intentar escribir en la matriz.
Una desventaja de este enfoque es que deja abierta la posibilidad de un error en tiempo de ejecución que un sistema de tipos más estricto podría haber detectado en tiempo de compilación. Además, perjudica el rendimiento porque cada escritura en una matriz requiere una comprobación adicional en tiempo de ejecución.
Con la incorporación de los genéricos, Java [4] : 126–129 y C# ahora ofrecen formas de escribir este tipo de función polimórfica sin depender de la covarianza. Las funciones de comparación y mezcla de matrices pueden recibir los tipos parametrizados
< T > booleano equalArrays ( T [] a1 , T [] a2 ); < T > void shuffleArray ( T [] a ); Como alternativa, para garantizar que un método C# acceda a una colección de forma de solo lectura, se puede usar la interfaz en lugar de pasarle una matriz .IEnumerable<object>object[]
Los lenguajes con funciones de primera clase tienen tipos de funciones como "una función que espera un Gato y devuelve un Animal" (escrito en sintaxis OCaml o en sintaxis C# ).cat -> animalFunc<Cat,Animal>
Esos lenguajes también necesitan especificar cuándo un tipo de función es un subtipo de otro, es decir, cuándo es seguro usar una función de un tipo en un contexto que espera una función de un tipo diferente. Es seguro sustituir una función f por una función g si f acepta un tipo de argumento más general y devuelve un tipo más específico que g . Por ejemplo, las funciones de tipo , , y se pueden usar dondequiera que se espere a. (Se puede comparar esto con el principio de robustez de la comunicación: "sé liberal en lo que aceptas y conservador en lo que produce"). La regla general es:animal -> catcat -> catanimal -> animalcat -> animal
Usando la notación de reglas de inferencia, la misma regla se puede escribir como:
En otras palabras, el constructor de tipo → es contravariante en el tipo de parámetro (entrada) y covariante en el tipo de retorno (salida) . Esta regla fue enunciada formalmente por primera vez por John C. Reynolds [ 5] y popularizada en un artículo de Luca Cardelli [6] .
Cuando se trabaja con funciones que toman funciones como argumentos , esta regla se puede aplicar varias veces. Por ejemplo, al aplicar la regla dos veces, vemos que si . En otras palabras, el tipo es covariante en la posición de . Para tipos complicados puede resultar confuso rastrear mentalmente por qué una especialización de tipo dada es o no segura para el tipo, pero es fácil calcular qué posiciones son covariantes y contravariantes: una posición es covariante si está en el lado izquierdo de un número par de flechas que se aplican a ella.
Cuando una subclase reemplaza un método en una superclase, el compilador debe verificar que el método que reemplaza tenga el tipo correcto. Si bien algunos lenguajes requieren que el tipo coincida exactamente con el tipo en la superclase (invariancia), también es seguro permitir que el método que reemplaza tenga un tipo "mejor". Según la regla de subtipificación habitual para los tipos de función, esto significa que el método que reemplaza debe devolver un tipo más específico (covarianza del tipo de retorno) y aceptar un argumento más general (contravarianza del tipo de parámetro). En la notación UML , las posibilidades son las siguientes (donde la Clase B es la subclase que extiende la Clase A, que es la superclase):
Para dar un ejemplo concreto, supongamos que estamos escribiendo una clase para modelar un refugio para animales . Suponemos que Cates una subclase de Animaly que tenemos una clase base (usando la sintaxis de Java).

clase RefugioAnimal { Animal getAnimalForAdoption () { // ... } void putAnimal ( Animal animal ) { //... } } Ahora la pregunta es: si subclasificamos AnimalShelter, ¿qué tipos podemos darle a getAnimalForAdoptiony putAnimal?
En un lenguaje que permite tipos de retorno covariantes , una clase derivada puede anular el getAnimalForAdoptionmétodo para devolver un tipo más específico:
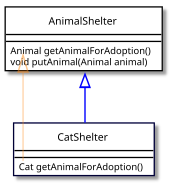
la clase CatShelter extiende AnimalShelter { Gato getAnimalForAdoption () { return new Gato (); } } Entre los principales lenguajes OO, Java , C++ y C# (a partir de la versión 9.0 [7] ) admiten tipos de retorno covariantes. La incorporación del tipo de retorno covariante fue una de las primeras modificaciones del lenguaje C++ aprobadas por el comité de estándares en 1998. [8] Scala y D también admiten tipos de retorno covariantes.
De manera similar, es seguro permitir que un método de reemplazo acepte un argumento más general que el método en la clase base:

clase CatShelter extiende AnimalShelter { void putAnimal ( Object animal ) { // ... } } En realidad, solo unos pocos lenguajes orientados a objetos lo permiten (por ejemplo, Python cuando se verifica el tipo con mypy). C++, Java y la mayoría de los demás lenguajes que admiten la sobrecarga o el sombreado interpretarían esto como un método con un nombre sobrecargado o sombreado.
Sin embargo, Sather admitía tanto la covarianza como la contravarianza. La convención de llamada para los métodos anulados es covariante sin parámetros y valores de retorno, y contravariante con parámetros normales (con la moda en ).
Un par de lenguajes convencionales, Eiffel y Dart [9], permiten que los parámetros de un método de reemplazo tengan un tipo más específico que el método en la superclase (covarianza de tipo de parámetro). Por lo tanto, el siguiente código Dart verificaría el tipo, putAnimalreemplazando el método en la clase base:

la clase CatShelter extiende AnimalShelter { void putAnimal ( covariante Gato animal ) { // ... } } Esto no es seguro en cuanto a tipos. Al convertir a CatShelteren an AnimalShelter, se puede intentar colocar un perro en un refugio para gatos. Esto no cumple con CatShelterlas restricciones de parámetros y dará como resultado un error de tiempo de ejecución. La falta de seguridad de tipos (conocida como el "problema del silbido" en la comunidad Eiffel, donde "gato" o "CAT" es una Disponibilidad o Tipo Cambiado) ha sido un problema de larga data. A lo largo de los años, se han propuesto varias combinaciones de análisis estático global, análisis estático local y nuevas características del lenguaje para remediarlo, [10] [11] y estas se han implementado en algunos compiladores de Eiffel.
A pesar del problema de seguridad de tipos, los diseñadores de Eiffel consideran que los tipos de parámetros covariantes son cruciales para modelar los requisitos del mundo real. [11] El refugio para gatos ilustra un fenómeno común: es una especie de refugio para animales pero tiene restricciones adicionales , y parece razonable usar herencia y tipos de parámetros restringidos para modelarlo. Al proponer este uso de la herencia, los diseñadores de Eiffel rechazan el principio de sustitución de Liskov , que establece que los objetos de las subclases siempre deben estar menos restringidos que los objetos de su superclase.
Otro ejemplo de un lenguaje convencional que permite la covarianza en los parámetros de los métodos es PHP en lo que respecta a los constructores de clases. En el siguiente ejemplo, se acepta el método __construct(), a pesar de que el parámetro del método es covariante con el parámetro del método principal. Si este método fuera distinto de __construct(), se produciría un error:
Interfaz AnimalInterface {}Interfaz DogInterface extiende AnimalInterface {}La clase Perro implementa DogInterface {}clase Mascota { función pública __construct ( AnimalInterface $animal ) {} } clase PetDog extiende Pet { función pública __construct ( DogInterface $dog ) { padre :: __construct ( $dog ); } } Otro ejemplo en el que los parámetros covariantes parecen ser útiles son los denominados métodos binarios, es decir, métodos en los que se espera que el parámetro sea del mismo tipo que el objeto sobre el que se invoca el método. Un ejemplo es el compareTométodo: comprueba si viene antes o después en algún orden, pero la forma de comparar, por ejemplo, dos números racionales será diferente de la forma de comparar dos cadenas. Otros ejemplos comunes de métodos binarios incluyen pruebas de igualdad, operaciones aritméticas y operaciones de conjunto como subconjunto y unión.a.compareTo(b)ab
En versiones anteriores de Java, el método de comparación se especificaba como una interfaz Comparable:
Interfaz comparable { int compareTo ( Objeto o ); } La desventaja de esto es que el método está especificado para tomar un argumento de tipo Object. Una implementación típica primero convertiría este argumento (generando un error si no es del tipo esperado):
clase RationalNumber implementa Comparable { int numerador ; int denominador ; // ... público int compareTo ( Object other ) { RationalNumber otherNum = ( RationalNumber ) other ; devuelve Integer.compare ( numerador * otherNum.denominador , otherNum.numerador * denominador ) ; } } compareToEn un lenguaje con parámetros covariantes, se podría dar directamente al argumento to el tipo deseado RationalNumber, ocultando la conversión de tipos. (Por supuesto, esto aún generaría un error de tiempo de ejecución si compareToluego se llamara en, por ejemplo, a String).
Otras características del lenguaje pueden proporcionar los beneficios aparentes de los parámetros covariantes mientras preservan la sustituibilidad de Liskov.
En un lenguaje con genéricos (también conocido como polimorfismo paramétrico ) y cuantificación acotada , los ejemplos anteriores se pueden escribir de manera segura para los tipos. [12] En lugar de definir AnimalShelter, definimos una clase parametrizada . (Una desventaja de esto es que el implementador de la clase base necesita prever qué tipos deberán especializarse en las subclases).Shelter<T>
clase Refugio < T extiende Animal > { T obtenerAnimalParaAdopcion () { // ... } void putAnimal ( T animal ) { // ... } } la clase CatShelter extiende Shelter < Cat > { Gato getAnimalForAdoption () { // ... } void putAnimal ( gato animal ) { // ... } } De manera similar, en versiones recientes de Java Comparablese ha parametrizado la interfaz, lo que permite omitir el downcast de forma segura:
la clase RationalNumber implementa Comparable < RationalNumber > { int numerador ; int denominador ; // ... public int compareTo ( RationalNumber otherNum ) { return Integer . compare ( numerador * otherNum . denominador , otherNum . numerador * denominador ); } } Otra característica del lenguaje que puede resultar de ayuda es el envío múltiple . Una de las razones por las que los métodos binarios son difíciles de escribir es que en una llamada como , la selección de la implementación correcta de realmente depende del tipo de tiempo de ejecución de y , pero en un lenguaje orientado a objetos convencional solo se tiene en cuenta el tipo de tiempo de ejecución de . En un lenguaje con envío múltiple al estilo de Common Lisp Object System (CLOS) , el método de comparación podría escribirse como una función genérica donde ambos argumentos se utilizan para la selección del método.a.compareTo(b)compareToaba
Giuseppe Castagna [13] observó que en un lenguaje tipado con envío múltiple, una función genérica puede tener algunos parámetros que controlan el envío y algunos parámetros "sobrantes" que no lo hacen. Debido a que la regla de selección de método elige el método aplicable más específico, si un método anula a otro método, entonces el método que lo anula tendrá tipos más específicos para los parámetros de control. Por otro lado, para garantizar la seguridad de tipos, el lenguaje aún debe requerir que los parámetros sobrantes sean al menos tan generales. Usando la terminología anterior, los tipos usados para la selección del método en tiempo de ejecución son covariantes mientras que los tipos no usados para la selección del método en tiempo de ejecución del método son contravariantes. Los lenguajes convencionales de envío único como Java también obedecen esta regla: solo se usa un argumento para la selección del método (el objeto receptor, pasado a un método como argumento oculto this), y de hecho el tipo de thises más especializado dentro de los métodos que anulan que en la superclase.
Castagna sugiere que los ejemplos en los que los tipos de parámetros covariantes son superiores (en particular, los métodos binarios) se deben manejar mediante el envío múltiple, que es naturalmente covariante. Sin embargo, la mayoría de los lenguajes de programación no admiten el envío múltiple.
La siguiente tabla resume las reglas para anular métodos en los lenguajes analizados anteriormente.
En los lenguajes de programación que admiten genéricos (también conocidos como polimorfismo paramétrico ), el programador puede ampliar el sistema de tipos con nuevos constructores. Por ejemplo, una interfaz de C# como permite construir nuevos tipos como o . Entonces surge la pregunta de cuál debería ser la varianza de estos constructores de tipos.IList<T>IList<Animal>IList<Cat>
Existen dos enfoques principales. En lenguajes con anotaciones de variación en el sitio de declaración (por ejemplo, C# ), el programador anota la definición de un tipo genérico con la variación deseada de sus parámetros de tipo. Con anotaciones de variación en el sitio de uso (por ejemplo, Java ), el programador anota los lugares donde se instancia un tipo genérico.
Los lenguajes más populares con anotaciones de varianza en el sitio de declaración son C# y Kotlin (que utilizan las palabras clave outy in), y Scala y OCaml (que utilizan las palabras clave +y -). C# solo permite anotaciones de varianza para tipos de interfaz, mientras que Kotlin, Scala y OCaml las permiten tanto para tipos de interfaz como para tipos de datos concretos.
En C#, cada parámetro de tipo de una interfaz genérica se puede marcar como covariante ( out), contravariante ( in) o invariante (sin anotación). Por ejemplo, podemos definir una interfaz de iteradores de solo lectura y declararla como covariante (out) en su parámetro de tipo.IEnumerator<T>
interfaz IEnumerator < out T > { T Current { obtener ; } bool MoveNext (); } Con esta declaración, IEnumeratorse tratará como covariante en su parámetro de tipo, por ejemplo, es un subtipo de .IEnumerator<Cat>IEnumerator<Animal>
El verificador de tipos hace cumplir que cada declaración de método en una interfaz solo mencione los parámetros de tipo de una manera consistente con las anotaciones in/ out. Es decir, un parámetro que se declaró covariante no debe aparecer en ninguna posición contravariante (donde una posición es contravariante si aparece bajo un número impar de constructores de tipo contravariante). La regla precisa [14] [15] es que los tipos de retorno de todos los métodos en la interfaz deben ser válidos covariantemente y todos los tipos de parámetros de método deben ser válidos contravariantemente , donde S-ly válido se define de la siguiente manera:
Tes válido covariantemente si no fue marcado in, y válido contravariantemente si no fue marcado out.A[]AG<A1, A2, ..., An>AiGse declara covariante, oGse declara contravariante, oGse declara invariante.Como ejemplo de cómo se aplican estas reglas, consideremos la interfaz. IList<T>
interfaz IList < T > { void Insertar ( int índice , T elemento ); IEnumerator < T > ObtenerEnumerador (); } El tipo de parámetro Tde Insertdebe ser válido contravariantemente, es decir, el parámetro de tipo Tno debe estar etiquetado out. De manera similar, el tipo de resultado de debe ser válido covariantemente, es decir (ya que es una interfaz covariante) el tipo debe ser válido covariantemente, es decir, el parámetro de tipo no debe estar etiquetado . Esto muestra que no se permite que la interfaz se marque como covariante o contravariante.IEnumerator<T>GetEnumeratorIEnumeratorTTinIList
En el caso común de una estructura de datos genérica como IList, estas restricciones significan que un outparámetro solo se puede usar para métodos que extraen datos de la estructura, y un inparámetro solo se puede usar para métodos que introducen datos en la estructura, de ahí la elección de palabras clave.
C# permite anotaciones de varianza en los parámetros de las interfaces, pero no en los parámetros de las clases. Debido a que los campos en las clases de C# son siempre mutables, las clases con parámetros de varianza en C# no serían muy útiles. Pero los lenguajes que enfatizan los datos inmutables pueden hacer un buen uso de los tipos de datos covariantes. Por ejemplo, en todos los lenguajes de Scala , Kotlin y OCaml, el tipo de lista inmutable es covariant: es un subtipo de .List[Cat]List[Animal]
Las reglas de Scala para comprobar las anotaciones de varianza son básicamente las mismas que las de C#. Sin embargo, hay algunos modismos que se aplican a las estructuras de datos inmutables en particular. Se ilustran con el siguiente (extracto de) definición de la clase.List[A]
clase abstracta sellada Lista [ + A ] extiende AbstractSeq [ A ] { def cabeza : A def cola : Lista [ A ] /** Agrega un elemento al comienzo de esta lista. */ def :: [ B >: A ] ( x : B ): List [ B ] = new scala . collection . immutable . :: ( x , this ) /** ... */ } En primer lugar, los miembros de clase que tienen un tipo variante deben ser inmutables. Aquí, headtiene el tipo A, que se declaró covariante ( +), y de hecho headse declaró como un método ( def). Intentar declararlo como un campo mutable ( var) sería rechazado como error de tipo.
En segundo lugar, incluso si una estructura de datos es inmutable, a menudo tendrá métodos en los que el tipo del parámetro aparece de forma contravariante. Por ejemplo, considere el método ::que agrega un elemento al principio de una lista. (La implementación funciona creando un nuevo objeto de la clase :: con nombre similar , la clase de listas no vacías). El tipo más obvio para asignarle sería
def : :( x : A ): Lista [ A ] Sin embargo, esto sería un error de tipo, porque el parámetro covariante Aaparece en una posición contravariante (como un parámetro de función). Pero hay un truco para evitar este problema. Damos ::un tipo más general, que permite agregar un elemento de cualquier tipo B
siempre que Bsea un supertipo de A. Tenga en cuenta que esto se basa en Listser covariante, ya que this tiene tipo y lo tratamos como si tuviera tipo . A primera vista, puede que no sea obvio que el tipo generalizado sea correcto, pero si el programador comienza con la declaración de tipo más simple, los errores de tipo señalarán el lugar que necesita ser generalizado.List[A]List[B]
Es posible diseñar un sistema de tipos en el que el compilador infiera automáticamente las mejores anotaciones de varianza posibles para todos los parámetros de tipo de datos. [16] Sin embargo, el análisis puede volverse complejo por varias razones. Primero, el análisis no es local ya que la varianza de una interfaz Idepende de la varianza de todas las interfaces que Imenciona. Segundo, para obtener las mejores soluciones únicas, el sistema de tipos debe permitir parámetros bivariantes (que son simultáneamente covariantes y contravariantes). Y finalmente, la varianza de los parámetros de tipo debería ser, sin lugar a dudas, una elección deliberada por parte del diseñador de una interfaz, no algo que simplemente sucede.
Por estas razones [17] la mayoría de los lenguajes realizan muy poca inferencia de varianza. C# y Scala no infieren ninguna anotación de varianza. OCaml puede inferir la varianza de tipos de datos concretos parametrizados, pero el programador debe especificar explícitamente la varianza de los tipos abstractos (interfaces).
Por ejemplo, considere un tipo de datos OCaml Tque envuelve una función
tipo ( ' a , ' b ) t = T de ( ' a -> ' b )El compilador inferirá automáticamente que Tes contravariante en el primer parámetro y covariante en el segundo. El programador también puede proporcionar anotaciones explícitas, que el compilador comprobará que se cumplen. Por lo tanto, la siguiente declaración es equivalente a la anterior:
tipo (- ' a , + ' b ) t = T de ( ' a -> ' b )Las anotaciones explícitas en OCaml resultan útiles al especificar interfaces. Por ejemplo, la interfaz de la biblioteca estándar para las tablas de asociación incluye una anotación que indica que el constructor del tipo de mapa es covariante en el tipo de resultado.Map.S
tipo de módulo S = tipo sig tipo clave (+ ' a ) t val vacío : ' a t val mem : clave -> ' a t -> bool ... fin Esto garantiza que eg sea un subtipo de .cat IntMap.tanimal IntMap.t
Una desventaja del enfoque de sitio de declaración es que muchos tipos de interfaz deben hacerse invariables. Por ejemplo, vimos anteriormente que IListnecesitaba ser invariable, porque contenía tanto Inserty GetEnumerator. Para exponer más variación, el diseñador de API podría proporcionar interfaces adicionales que proporcionen subconjuntos de los métodos disponibles (por ejemplo, una "lista de solo inserción" que solo proporcione Insert). Sin embargo, esto se vuelve difícil de manejar rápidamente.
La variación en el sitio de uso significa que la variación deseada se indica con una anotación en el sitio específico del código donde se utilizará el tipo. Esto ofrece a los usuarios de una clase más oportunidades para la subtipificación sin necesidad de que el diseñador de la clase defina varias interfaces con diferentes variaciones. En cambio, en el punto en que se crea una instancia de un tipo genérico en un tipo parametrizado real, el programador puede indicar que solo se utilizará un subconjunto de sus métodos. En efecto, cada definición de una clase genérica también pone a disposición interfaces para las partes covariantes y contravariantes de esa clase.
Java proporciona anotaciones de variación del sitio de uso a través de comodines , una forma restringida de tipos existenciales acotados . Un tipo parametrizado se puede instanciar mediante un comodín junto con un límite superior o inferior, p. ej . o . Un comodín sin acotar como es equivalente a . Un tipo de este tipo representa un tipo desconocido que satisface el límite. [4] : 139 Por ejemplo, si tiene el tipo , entonces el verificador de tipos aceptará?List<? extends Animal>List<? super Animal>List<?>List<? extends Object>List<X>XlList<? extends Animal>
Animal a = l . obtener ( 3 ); porque se sabe que el tipo Xes un subtipo de Animal, pero
l . agregar ( nuevo Animal ()); se rechazará como un error de tipo ya que an Animalno es necesariamente un X. En general, dada alguna interfaz , una referencia a an prohíbe usar métodos de la interfaz donde ocurre contravariantemente en el tipo del método. Por el contrario, si tuviera tipo se podría llamar pero no .I<T>I<? extends T>TlList<? super Animal>l.addl.get

Si bien los tipos parametrizados sin comodines en Java son invariantes (por ejemplo, no existe una relación de subtipo entre y ), los tipos comodín se pueden hacer más específicos especificando un límite más estricto. Por ejemplo, es un subtipo de . Esto muestra que los tipos comodín son covariantes en sus límites superiores (y también contravariantes en sus límites inferiores ). En total, dado un tipo comodín como , hay tres formas de formar un subtipo: especializando la clase , especificando un límite más estricto o reemplazando el comodín con un tipo específico (ver figura). [4] : 139 List<Cat>List<Animal>List<? extends Cat>List<? extends Animal>C<? extends T>CT?
Al aplicar dos de las tres formas de subtipificación anteriores, se hace posible, por ejemplo, pasar un argumento de tipo a un método que espera un . Este es el tipo de expresividad que resulta de los tipos de interfaz covariantes. El tipo actúa como un tipo de interfaz que contiene solo los métodos covariantes de , pero el implementador de no tuvo que definirlo de antemano.List<Cat>List<? extends Animal>List<? extends Animal>List<T>List<T>
En el caso común de una estructura de datos genérica IList, se utilizan parámetros covariantes para los métodos que extraen datos de la estructura, y parámetros contravariantes para los métodos que introducen datos en la estructura. La regla mnemotécnica para Producer Extends, Consumer Super (PECS), del libro Effective Java de Joshua Bloch, ofrece una forma sencilla de recordar cuándo utilizar la covarianza y la contravarianza. [4] : 141
Los comodines son flexibles, pero tienen un inconveniente. Si bien la variación en el sitio de uso significa que los diseñadores de API no necesitan considerar la variación de los parámetros de tipo en las interfaces, a menudo deben usar firmas de métodos más complicadas. Un ejemplo común involucra la Comparableinterfaz. [4] : 66 Supongamos que queremos escribir una función que encuentre el elemento más grande en una colección. Los elementos deben implementar el compareTométodo, [4] : 66 por lo que un primer intento podría ser
< T extiende Comparable < T >> T max ( Colección < T > coll ); Sin embargo, este tipo no es lo suficientemente general: se puede encontrar el máximo de a , pero no de a . El problema es que no implementa , sino la (mejor) interfaz . En Java, a diferencia de C#, no se considera un subtipo de . En cambio, se debe modificar el tipo de :Collection<Calendar>Collection<GregorianCalendar>GregorianCalendarComparable<GregorianCalendar>Comparable<Calendar>Comparable<Calendar>Comparable<GregorianCalendar>max
< T extiende Comparable <? super T >> T max ( Colección < T > coll ); El comodín acotado transmite la información que llama solo a métodos contravariantes de la interfaz. Este ejemplo en particular es frustrante porque todos los métodos en son contravariantes, por lo que esa condición es trivialmente verdadera. Un sistema de sitio de declaración podría manejar este ejemplo con menos desorden al anotar solo la definición de .? super TmaxComparableComparableComparable
El maxmétodo se puede modificar aún más utilizando un comodín con límite superior para el parámetro del método: [18]
< T extiende Comparable <? super T >> T max ( Colección <? extiende T > coll ); Las anotaciones de variación en el lugar de uso brindan una flexibilidad adicional, lo que permite que más programas realicen la verificación de tipos. Sin embargo, han sido criticadas por la complejidad que agregan al lenguaje, lo que genera firmas de tipos complicadas y mensajes de error.
Una forma de evaluar si la flexibilidad adicional es útil es ver si se utiliza en programas existentes. Un estudio de un gran conjunto de bibliotecas Java [16] descubrió que el 39% de las anotaciones con comodines podrían haberse reemplazado directamente por anotaciones en el sitio de declaración. Por lo tanto, el 61% restante es una indicación de los lugares en los que Java se beneficia de tener disponible el sistema de sitio de uso.
En un lenguaje de sitio de declaración, las bibliotecas deben exponer menos varianza o definir más interfaces. Por ejemplo, la biblioteca Scala Collections define tres interfaces independientes para las clases que emplean covarianza: una interfaz base covariante que contiene métodos comunes, una versión mutable invariante que agrega métodos con efectos secundarios y una versión inmutable covariante que puede especializar las implementaciones heredadas para explotar el uso compartido estructural. [19] Este diseño funciona bien con anotaciones de sitio de declaración, pero la gran cantidad de interfaces conlleva un costo de complejidad para los clientes de la biblioteca. Y modificar la interfaz de la biblioteca puede no ser una opción; en particular, uno de los objetivos al agregar genéricos a Java era mantener la compatibilidad binaria con versiones anteriores.
Por otro lado, los comodines de Java son complejos en sí mismos. En una presentación en una conferencia [20], Joshua Bloch los criticó por ser demasiado difíciles de entender y usar, afirmando que al agregar soporte para cierres "simplemente no podemos permitirnos otros comodines ". Las primeras versiones de Scala usaban anotaciones de varianza en el sitio de uso, pero los programadores las encontraron difíciles de usar en la práctica, mientras que las anotaciones en el sitio de declaración resultaron ser muy útiles al diseñar clases. [21] Las versiones posteriores de Scala agregaron tipos existenciales y comodines al estilo Java; sin embargo, según Martin Odersky , si no hubiera necesidad de interoperabilidad con Java, probablemente no se hubieran incluido. [22]
Ross Tate sostiene [23] que parte de la complejidad de los comodines de Java se debe a la decisión de codificar la varianza del sitio de uso utilizando una forma de tipos existenciales. Las propuestas originales [24] [25] utilizaban una sintaxis de propósito especial para las anotaciones de varianza, escribiendo en lugar del más detallado .List<+Animal>List<? extends Animal>
Dado que los comodines son una forma de tipos existenciales, se pueden utilizar para más cosas que simplemente la varianza. Un tipo como ("una lista de tipo desconocido" [26] ) permite que los objetos se pasen a métodos o se almacenen en campos sin especificar exactamente sus parámetros de tipo. Esto es particularmente valioso para clases como aquellas en las que la mayoría de los métodos no mencionan el parámetro de tipo.List<?>Class
Sin embargo, la inferencia de tipos para tipos existenciales es un problema difícil. Para el implementador del compilador, los comodines de Java plantean problemas con la terminación del verificador de tipos, la inferencia de argumentos de tipos y los programas ambiguos. [27] En general, es indeciso si un programa Java que utiliza genéricos está bien tipificado o no, [28] por lo que cualquier verificador de tipos tendrá que entrar en un bucle infinito o agotar el tiempo de espera para algunos programas. Para el programador, esto conduce a mensajes de error de tipo complicados. Java verifica los tipos de comodines reemplazando los comodines con nuevas variables de tipo (la llamada conversión de captura ). Esto puede hacer que los mensajes de error sean más difíciles de leer, porque se refieren a variables de tipo que el programador no escribió directamente. Por ejemplo, intentar agregar a Cata a dará un error comoList<? extends Animal>
El método List.add (capture#1) no es aplicable (el argumento real Cat no se puede convertir a capture#1 mediante la conversión de invocación del método)donde capture#1 es una nueva variable de tipo: La captura n.° 1 extiende Animal de la captura de ? extiende Animal
Dado que tanto las anotaciones del sitio de declaración como las del sitio de uso pueden ser útiles, algunos sistemas de tipos proporcionan ambas. [16] [23]
Estos términos provienen de la noción de funtores covariantes y contravariantes en la teoría de categorías . Considere la categoría cuyos objetos son tipos y cuyos morfismos representan la relación de subtipo ≤. (Este es un ejemplo de cómo cualquier conjunto parcialmente ordenado puede considerarse como una categoría). Entonces, por ejemplo, el constructor de tipo de función toma dos tipos p y r y crea un nuevo tipo p → r ; por lo que toma objetos en a objetos en . Por la regla de subtipificación para tipos de función, esta operación invierte ≤ para el primer parámetro y lo conserva para el segundo, por lo que es un funtor contravariante en el primer parámetro y un funtor covariante en el segundo.
I<T> = int: se puede introducir cualquier tipo en for Ty el resultado sigue siendo int.{{cite web}}: CS1 maint: location (link)