Curva de De Rham

Curva fractal continua obtenida como imagen del espacio de Cantor

En matemáticas , una curva de De Rham es una curva fractal continua obtenida como la imagen del espacio de Cantor o, equivalentemente, a partir de la expansión en base dos de los números reales en el intervalo unitario. Muchas curvas fractales conocidas, incluidas la función de Cantor , la curva de Cesáro-Faber ( curva C de Lévy ), la función del signo de interrogación de Minkowski , la curva del manjar blanco y la curva de Koch son ejemplos de curvas de De Rham. La forma general de la curva fue descrita por primera vez por Georges de Rham en 1957. ^[1]

Construcción

Consideremos un espacio métrico completo (generalmente ² con la distancia euclidiana habitual) y un par de mapas contractivos en M: ${\displaystyle (M,d)}$ ${\displaystyle \mathbb {R} }$

${\displaystyle d_{0}:\ M\to M}$

${\displaystyle d_{1}:\ M\to M.}$

Por el teorema del punto fijo de Banach , estos tienen puntos fijos y respectivamente. Sea x un número real en el intervalo , que tiene expansión binaria ${\displaystyle p_{0}}$ ${\displaystyle p_{1}}$ ${\displaystyle [0,1]}$

${\displaystyle x=\sum _{k=1}^{\infty }{\frac {b_{k}}{2^{k}}},}$

donde cada uno es 0 o 1. Considere el mapa ${\displaystyle b_{k}}$

${\displaystyle c_{x}:\ M\to M}$

definido por

${\displaystyle c_{x}=d_{b_{1}}\circ d_{b_{2}}\circ \cdots \circ d_{b_{k}}\circ \cdots ,}$

donde denota la composición de funciones . Se puede demostrar que cada una mapeará la cuenca común de atracción de y a un único punto en . La colección de puntos , parametrizada por un único parámetro real x , se conoce como la curva de De Rham. ${\displaystyle \circ }$ ${\displaystyle c_{x}}$ ${\displaystyle d_{0}}$ ${\displaystyle d_{1}}$ ${\displaystyle p_{x}}$ ${\displaystyle M}$ ${\displaystyle p_{x}}$

Condición de continuidad

La construcción en términos de dígitos binarios se puede entender de dos maneras distintas. Una es como una aplicación del espacio de Cantor a puntos distintos en el plano. El espacio de Cantor es el conjunto de todas las cadenas infinitamente largas de dígitos binarios. Es un espacio discreto y está desconectado . El espacio de Cantor se puede aplicar al intervalo real unitario tratando cada cadena como una expansión binaria de un número real. En esta aplicación, los racionales diádicos tienen dos representaciones distintas como cadenas de dígitos binarios. Por ejemplo, el número real un medio tiene dos expansiones binarias equivalentes: y Esto es análogo a cómo se tiene 0,999...=1,000... en expansiones decimales. Los dos puntos y son puntos distintos en el espacio de Cantor, pero ambos se asignan al número real un medio. De esta manera, los reales del intervalo unitario son una imagen continua del espacio de Cantor. ${\displaystyle h_{1}=0.1000\cdots }$ ${\displaystyle h_{0}=0.01111\cdots }$ ${\displaystyle h_{0}}$ ${\displaystyle h_{1}}$

La misma noción de continuidad se aplica a la curva de De Rham pidiendo que los puntos fijos estén emparejados, de modo que

${\displaystyle d_{0}(p_{1})=d_{1}(p_{0})}$

Con este emparejamiento, las expansiones binarias de los racionales diádicos siempre se asignan al mismo punto, lo que garantiza la continuidad en ese punto. Consideremos el comportamiento en la mitad. Para cualquier punto p en el plano, se tienen dos secuencias distintas:

${\displaystyle d_{0}\circ d_{1}\circ d_{1}\circ d_{1}\circ \cdots (p)}$

y

${\displaystyle d_{1}\circ d_{0}\circ d_{0}\circ d_{0}\circ \cdots (p)}$

correspondiente a las dos expansiones binarias y . Puesto que las dos aplicaciones son ambas contrayentes, la primera secuencia converge a y la segunda a . Si estas dos son iguales, entonces ambas expansiones binarias de 1/2 se asignan al mismo punto. Este argumento se puede repetir en cualquier racional diádico, asegurando así la continuidad en esos puntos. Los números reales que no son racionales diádicos tienen solo una única representación binaria, y de esto se sigue que la curva no puede ser discontinua en esos puntos. La curva de De Rham resultante es una función continua de x , en todo x . ${\displaystyle 1/2=0.01111\cdots }$ ${\displaystyle 1/2=0.1000\cdots }$ ${\displaystyle d_{0}(p_{1})}$ ${\displaystyle d_{1}(p_{0})}$ ${\displaystyle p_{x}}$

En general, las curvas de De Rham no son diferenciables.

Propiedades

Las curvas de De Rham son autosimilares por construcción, ya que

${\displaystyle p(x)=d_{0}(p(2x))}$para y ${\displaystyle x\in [0,1/2]}$

${\displaystyle p(x)=d_{1}(p(2x-1))}$para ${\displaystyle x\in [1/2,1].}$

Las autosimetrías de todas las curvas de De Rham están dadas por el monoide que describe las simetrías del árbol binario infinito o espacio de Cantor . Este llamado monoide de duplicación de período es un subconjunto del grupo modular .

La imagen de la curva, es decir, el conjunto de puntos , se puede obtener mediante un sistema de funciones iteradas utilizando el conjunto de aplicaciones de contracción . Pero el resultado de un sistema de funciones iteradas con dos aplicaciones de contracción es una curva de De Rham si y solo si las aplicaciones de contracción satisfacen la condición de continuidad. ${\displaystyle \{p(x),x\in [0,1]\}}$ ${\displaystyle \{d_{0},\ d_{1}\}}$

Se pueden encontrar ejemplos detallados y resueltos de las autosimilitudes en los artículos sobre la función de Cantor y sobre la función de signo de interrogación de Minkowski . Precisamente el mismo monoide de autosimilitudes, el monoide diádico , se aplica a toda curva de De Rham.

Clasificación y ejemplos

Los siguientes sistemas generan curvas continuas.

Curvas de Cesáro

Curva de Cesáro para a  = 0,3 +  i  0,3

Curva de Cesáro para a  = 0,5 +  i  0,5. Esta es la curva C de Lévy .

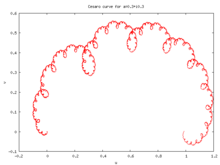
Las curvas de Cesàro , también conocidas como curvas de Cesàro-Faber o curvas de Lévy C , son curvas de De Rham generadas por transformaciones afines que conservan la orientación , con puntos fijos y . ${\displaystyle p_{0}=0}$ ${\displaystyle p_{1}=1}$

Debido a estas restricciones, las curvas de Cesàro están determinadas únicamente por un número complejo tal que y . ${\displaystyle a}$ ${\displaystyle |a|<1}$ ${\displaystyle |1-a|<1}$

Las aplicaciones de contracción y se definen entonces como funciones complejas en el plano complejo mediante: ${\displaystyle d_{0}}$ ${\displaystyle d_{1}}$

${\displaystyle d_{0}(z)=az}$

${\displaystyle d_{1}(z)=a+(1-a)z.}$

Para el valor de , la curva resultante es la curva C de Lévy . ${\displaystyle a=(1+i)/2}$

Curvas de Koch-Peano

Curva de Koch-Peano para a  = 0,6 +  i  0,37. Es una curva cercana a la de Koch , pero no exactamente igual .

Curva de Koch-Peano para a  = 0,6 +  i  0,45.

De manera similar, podemos definir la familia de curvas Koch-Peano como el conjunto de curvas de De Rham generadas por transformaciones afines que invierten la orientación, con puntos fijos y . ${\displaystyle p_{0}=0}$ ${\displaystyle p_{1}=1}$

Estas aplicaciones se expresan en el plano complejo como una función de , el conjugado complejo de : ${\displaystyle {\overline {z}}}$ ${\displaystyle z}$

${\displaystyle d_{0}(z)=a{\overline {z}}}$

${\displaystyle d_{1}(z)=a+(1-a){\overline {z}}.}$

El nombre de la familia proviene de sus dos miembros más famosos. La curva de Koch se obtiene al establecer:

${\displaystyle a_{\text{Koch}}={\frac {1}{2}}+i{\frac {\sqrt {3}}{6}},}$

Mientras que la curva de Peano corresponde a:

${\displaystyle a_{\text{Peano}}={\frac {(1+i)}{2}}.}$

La curva de De Rham para valores de apenas menos de uno se parece visualmente a la curva de Osgood . Estas dos curvas están estrechamente relacionadas, pero no son iguales. La curva de Osgood se obtiene por sustracción repetida de conjuntos y, por lo tanto, es un conjunto perfecto , muy parecido al propio conjunto de Cantor . La construcción del conjunto de Osgood requiere que se resten triángulos progresivamente más pequeños, dejando atrás un conjunto "gordo" de medida distinta de cero; la construcción es análoga al conjunto gordo de Cantor , que tiene una medida distinta de cero . Por el contrario, la curva de De Rham no es "gorda"; la construcción no ofrece una manera de "engordar" los "segmentos de línea" que corren "entre" los racionales diádicos. ${\displaystyle a=(1+ib)/2}$ ${\displaystyle b}$

Mapas afines generales

Curva de Rham afín genérica

Curva de Rham afín genérica

Curva de Rham afín genérica

Curva de Rham afín genérica

Las curvas de Cesáro-Faber y de Peano-Koch son casos especiales del caso general de un par de transformaciones lineales afines en el plano complejo. Al fijar un punto final de la curva en 0 y el otro en 1, se obtiene el caso general iterando sobre las dos transformadas.

${\displaystyle d_{0}={\begin{pmatrix}1&0&0\\0&\alpha &\delta \\0&\beta &\varepsilon \end{pmatrix}}}$

y

${\displaystyle d_{1}={\begin{pmatrix}1&0&0\\\alpha &1-\alpha &\zeta \\\beta &-\beta &\eta \end{pmatrix}}.}$

Al ser transformaciones afines , estas transformaciones actúan sobre un punto del plano 2-D actuando sobre el vector ${\displaystyle (u,v)}$

${\displaystyle {\begin{pmatrix}1\\u\\v\end{pmatrix}}.}$

Se puede ver que el punto medio de la curva se ubica en ; los otros cuatro parámetros pueden variarse para crear una gran variedad de curvas. ${\displaystyle (u,v)=(\alpha ,\beta )}$

La curva de manjar blanco del parámetro se puede obtener estableciendo , y . Es decir: ${\displaystyle w}$ ${\displaystyle \alpha =\beta =1/2}$ ${\displaystyle \delta =\zeta =0}$ ${\displaystyle \varepsilon =\eta =w}$

${\displaystyle d_{0}={\begin{pmatrix}1&0&0\\0&1/2&0\\0&1/2&w\end{pmatrix}}}$

y

${\displaystyle d_{1}={\begin{pmatrix}1&0&0\\1/2&1/2&0\\1/2&-1/2&w\end{pmatrix}}.}$

Dado que la curva de manjar blanco para el parámetro es una parábola de la ecuación , esto ilustra el hecho de que, en algunas ocasiones, las curvas de De Rham pueden ser suaves. ${\displaystyle w=1/4}$ ${\displaystyle f(x)=4x(1-x)}$

Función de signo de interrogación de Minkowski

La función de signo de interrogación de Minkowski se genera mediante el par de mapas

${\displaystyle d_{0}(z)={\frac {z}{z+1}}}$

y

${\displaystyle d_{1}(z)={\frac {1}{2-z}}.}$

No-ejemplos

Dadas dos funciones cualesquiera y , se puede definir una aplicación del espacio de Cantor , mediante la iteración repetida de los dígitos, exactamente de la misma manera que para las curvas de De Rham. En general, el resultado no será una curva de De Rham, cuando no se cumplen los términos de la condición de continuidad. Por lo tanto, hay muchos conjuntos que podrían estar en correspondencia uno a uno con el espacio de Cantor, cuyos puntos pueden etiquetarse de forma única mediante puntos en el espacio de Cantor; sin embargo, estas no son curvas de De Rham, cuando los racionales diádicos no se asignan al mismo punto. ${\displaystyle d_{0}}$ ${\displaystyle d_{1}}$

Conjunto de Julia del conjunto de Mandelbrot

El conjunto de Mandelbrot se genera mediante una ecuación iterada que duplica el período . El conjunto de Julia correspondiente se obtiene iterando en la dirección opuesta. Esto se hace escribiendo , lo que da dos raíces distintas de las que "proviene" la iteración hacia adelante . Estas dos raíces se pueden distinguir como ${\displaystyle z_{n+1}=z_{n}^{2}+c.}$ ${\displaystyle z_{n}=\pm {\sqrt {z_{n+1}-c}}}$ ${\displaystyle z_{n+1}}$

${\displaystyle d_{0}(z)=+{\sqrt {z-c}}}$

y

${\displaystyle d_{1}(z)=-{\sqrt {z-c}}.}$

Fijando el número complejo , el resultado es el conjunto de Julia para ese valor de . Esta curva es continua cuando está dentro del conjunto de Mandelbrot; en caso contrario, es un polvo de puntos desconectado. Sin embargo, la razón de la continuidad no se debe a la condición de De Rham, ya que, en general, los puntos correspondientes a los racionales diádicos están muy alejados entre sí. De hecho, esta propiedad puede utilizarse para definir una noción de "opuestos polares", de puntos conjugados en el conjunto de Julia. ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle c}$

Generalizaciones

Es fácil generalizar la definición utilizando más de dos aplicaciones de contracción. Si se utilizan n aplicaciones, entonces se debe utilizar la descomposición n -aria de x en lugar de la expansión binaria de números reales . La condición de continuidad se debe generalizar en:

${\displaystyle d_{i}(p_{n-1})=d_{i+1}(p_{0})}$, para ${\displaystyle i=0\ldots n-2.}$

Esta condición de continuidad se puede entender con el siguiente ejemplo. Supongamos que estamos trabajando en base 10. Entonces tenemos (famosamente) que 0,999...= 1,000... que es una ecuación de continuidad que debe aplicarse en cada uno de esos espacios. Es decir, dados los dígitos decimales con , tenemos ${\displaystyle b_{1},b_{2},\cdots ,b_{k}}$ ${\displaystyle b_{k}\neq 9}$

${\displaystyle b_{1},b_{2},\cdots ,b_{k},9,9,9,\cdots =b_{1},b_{2},\cdots ,b_{k}+1,0,0,0,\cdots }$

Esta generalización permite, por ejemplo, producir la curva de punta de flecha de Sierpiński (cuya imagen es el triángulo de Sierpiński ), utilizando las aplicaciones de contracción de un sistema de funciones iteradas que produce el triángulo de Sierpiński.

Curvas multifractales

Ornstein y otros describen un sistema multifractal , donde en lugar de trabajar en una base fija, se trabaja en una base variable.

Considere el espacio del producto de espacios discretos de base variable ${\displaystyle m_{n}}$

${\displaystyle \Omega =\prod _{n\in \mathbb {N} }A_{n}}$

para el grupo cíclico , para un entero. Cualquier número real en el intervalo unitario se puede desarrollar en una secuencia tal que cada . Más precisamente, un número real se escribe como ${\displaystyle A_{n}=\mathbb {Z} /m_{n}\mathbb {Z} =\{0,1,\cdots ,m_{n}-1\}}$ ${\displaystyle m_{n}\geq 2}$ ${\displaystyle (a_{1},a_{2},a_{3},\cdots )}$ ${\displaystyle a_{n}\in A_{n}}$ ${\displaystyle 0\leq x\leq 1}$

${\displaystyle x=\sum _{n=1}^{\infty }{\frac {a_{n}}{\prod _{k=1}^{n}m_{k}}}}$

Esta expansión no es única, si todas pasan por algún punto . En este caso, se tiene que ${\displaystyle a_{n}=0}$ ${\displaystyle K<n}$

${\displaystyle a_{1},a_{2},\cdots ,a_{K},0,0,\cdots =a_{1},a_{2},\cdots ,a_{K}-1,m_{K+1}-1,m_{K+2}-1,\cdots }$

Estos puntos son análogos a los racionales diádicos en la expansión diádica, y las ecuaciones de continuidad de la curva deben aplicarse en estos puntos.

Para cada , se deben especificar dos cosas: un conjunto de dos puntos y y un conjunto de funciones (con ). La condición de continuidad es entonces la anterior, ${\displaystyle A_{n}}$ ${\displaystyle p_{0}^{(n)}}$ ${\displaystyle p_{1}^{(n)}}$ ${\displaystyle m_{n}}$ ${\displaystyle d_{j}^{(n)}(z)}$ ${\displaystyle j\in A_{n}}$

${\displaystyle d_{j}^{(n)}(p_{1}^{(n+1)})=d_{j+1}^{(n)}(p_{0}^{(n+1)})}$, para ${\displaystyle j=0,\cdots ,m_{n}-2.}$

El ejemplo original de Ornstein utilizado

${\displaystyle \Omega =\left(\mathbb {Z} /2\mathbb {Z} \right)\times \left(\mathbb {Z} /3\mathbb {Z} \right)\times \left(\mathbb {Z} /4\mathbb {Z} \right)\times \cdots }$

Véase también

• Sistema de funciones iteradas
• Función refinable
• Grupo modular
• Grupo fucsia

Referencias

1. Georges de Rham, Sur quelques courbes definies par des ecuaciones funcionales . Univ. y Politec. Turín. Desgarrar. Sem. Mateo, 1957, 16, 101 –113

Lectura adicional

• Georges de Rham, Sobre algunas curvas definidas por ecuaciones funcionales (1957), reimpreso en Classics on Fractals , ed. Gerald A. Edgar (Addison-Wesley, 1993), págs. 285–298.
• Linas Vepstas, Una galería de curvas de De Rham , (2006).
• Linas Vepstas, Simetrías de mapas de duplicación de períodos , (2006). (Una exploración general de la simetría de grupo modular en curvas fractales.)