Correlación parcial

Concepto en teoría de probabilidad y estadística

En teoría de probabilidad y estadística , la correlación parcial mide el grado de asociación entre dos variables aleatorias , con el efecto de un conjunto de variables aleatorias de control eliminadas. Al determinar la relación numérica entre dos variables de interés, el uso de su coeficiente de correlación dará resultados engañosos si hay otra variable de confusión que esté numéricamente relacionada con ambas variables de interés. Esta información engañosa se puede evitar controlando la variable de confusión, lo que se hace calculando el coeficiente de correlación parcial. Esta es precisamente la motivación para incluir otras variables del lado derecho en una regresión múltiple ; pero mientras que la regresión múltiple da resultados imparciales para el tamaño del efecto , no da un valor numérico de una medida de la fuerza de la relación entre las dos variables de interés.

Por ejemplo, si se dan datos económicos sobre el consumo, los ingresos y la riqueza de varias personas, se puede considerar la relación entre el consumo y los ingresos. Si no se tiene en cuenta la riqueza al calcular un coeficiente de correlación entre el consumo y los ingresos, se obtendría un resultado engañoso, ya que los ingresos podrían estar relacionados numéricamente con la riqueza, que a su vez podría estar relacionada numéricamente con el consumo; una correlación medida entre el consumo y los ingresos podría estar contaminada por estas otras correlaciones. El uso de una correlación parcial evita este problema.

Al igual que el coeficiente de correlación, el coeficiente de correlación parcial toma un valor en el rango de –1 a 1. El valor –1 transmite una correlación negativa perfecta controlando algunas variables (es decir, una relación lineal exacta en la que los valores más altos de una variable están asociados con valores más bajos de la otra); el valor 1 transmite una relación lineal positiva perfecta, y el valor 0 transmite que no hay relación lineal.

La correlación parcial coincide con la correlación condicional si las variables aleatorias se distribuyen conjuntamente como distribución normal multivariada , otra elíptica , hipergeométrica multivariada , hipergeométrica negativa multivariada , multinomial o de Dirichlet , pero no en general en otros casos. ^[1]

Definición formal

Formalmente, la correlación parcial entre X e Y dado un conjunto de n variables de control Z = { Z ₁ , Z ₂ , ..., Z _n }, escrita ρ _{XY · Z} , es la correlación entre los residuos e _X y e _Y resultantes de la regresión lineal de X con Z y de Y con Z , respectivamente. La correlación parcial de primer orden (es decir, cuando n = 1) es la diferencia entre una correlación y el producto de las correlaciones removibles dividido por el producto de los coeficientes de alienación de las correlaciones removibles. El coeficiente de alienación y su relación con la varianza conjunta a través de la correlación están disponibles en Guilford (1973, pp. 344–345). ^[2]

Cálculo

Usando regresión lineal

Una forma sencilla de calcular la correlación parcial de la muestra para algunos datos es resolver los dos problemas de regresión lineal asociados y calcular la correlación entre los residuos. Sean X e Y variables aleatorias que toman valores reales, y sea Z la variable aleatoria de valor vectorial n -dimensional. Sean x _i , y _i y z _i las i -ésimas observaciones de alguna distribución de probabilidad conjunta sobre variables aleatorias reales X , Y y Z , con z _i aumentado con un 1 para permitir un término constante en la regresión. Resolver el problema de regresión lineal equivale a encontrar vectores de coeficientes de regresión ( n + 1)-dimensionales y tales que ${\displaystyle N}$ ${\displaystyle \mathbf {w} _{X}^{*}}$ ${\displaystyle \mathbf {w} _{Y}^{*}}$

${\displaystyle \mathbf {w} _{X}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(x_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}}$

${\displaystyle \mathbf {w} _{Y}^{*}=\arg \min _{\mathbf {w} }\left\{\sum _{i=1}^{N}(y_{i}-\langle \mathbf {w} ,\mathbf {z} _{i}\rangle )^{2}\right\}}$

donde es el número de observaciones, y es el producto escalar entre los vectores y . ${\displaystyle N}$ ${\displaystyle \langle \mathbf {w} ,\mathbf {z} _{i}\rangle }$ ${\displaystyle \mathbf {w} }$ ${\displaystyle \mathbf {z} _{i}}$

Los residuos son entonces

${\displaystyle e_{X,i}=x_{i}-\langle \mathbf {w} _{X}^{*},\mathbf {z} _{i}\rangle }$

${\displaystyle e_{Y,i}=y_{i}-\langle \mathbf {w} _{Y}^{*},\mathbf {z} _{i}\rangle }$

y la correlación parcial de la muestra se da entonces mediante la fórmula habitual para la correlación de la muestra , pero entre estos nuevos valores derivados :

${\displaystyle {\begin{aligned}{\hat {\rho }}_{XY\cdot \mathbf {Z} }&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}-\sum _{i=1}^{N}e_{X,i}\sum _{i=1}^{N}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}-\left(\sum _{i=1}^{N}e_{X,i}\right)^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}-\left(\sum _{i=1}^{N}e_{Y,i}\right)^{2}}}}}\\&={\frac {N\sum _{i=1}^{N}e_{X,i}e_{Y,i}}{{\sqrt {N\sum _{i=1}^{N}e_{X,i}^{2}}}~{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^{2}}}}}.\end{aligned}}}$

En la primera expresión, los tres términos después de los signos menos son todos iguales a 0, ya que cada uno contiene la suma de los residuos de una regresión de mínimos cuadrados ordinaria .

Ejemplo

Considere los siguientes datos sobre tres variables, X , Y y Z :

El cálculo del coeficiente de correlación de Pearson entre las variables X e Y da como resultado aproximadamente 0,970, mientras que el cálculo de la correlación parcial entre X e Y , utilizando la fórmula dada anteriormente, da como resultado una correlación parcial de 0,919. Los cálculos se realizaron utilizando R con el siguiente código.

> X <- c ( 2 , 4 , 15 , 20 ) > Y < - c ( 1 , 2 , 3 , 4 ) > Z < - c ( 0 , 0 , 1 , 1 ) > mm1 <- lm ( X ~ Z ) > res1 <- mm1 $ residuales > mm2 <- lm ( Y ~ Z ) > res2 <- mm2 $ residuales > cor ( res1 , res2 ) [1] 0.919145 > cor ( X , Y ) [1] 0.9695016 > generalCorr :: parcorMany ( cbind ( X , Y , Z ))  nami namj partij partji rijMrji [1,] "X" "Y" "0.8844" "1" "-0.1156" [2,] "X" "Z" "0,1581" "1" "-0,8419"               

La parte inferior del código anterior informa que el coeficiente de correlación parcial no lineal generalizado entre X e Y después de eliminar el efecto no lineal de Z es 0,8844. Además, el coeficiente de correlación parcial generalizado entre X y Z después de eliminar el efecto no lineal de Y es 0,1581. Consulte el paquete R `generalCorr' y sus viñetas para obtener más detalles. La simulación y otros detalles se encuentran en Vinod (2017) "Generalized correlation and kernel causality with applications in development economics", Communications in Statistics - Simulation and Computation, vol. 46, [4513, 4534], disponible en línea: 29 de diciembre de 2015, URL https://doi.org/10.1080/03610918.2015.1122048.

Usando la fórmula recursiva

La resolución de problemas de regresión lineal puede resultar costosa en términos computacionales. En realidad, la correlación parcial de orden n (es decir, con | Z | = n ) se puede calcular fácilmente a partir de tres correlaciones parciales de orden ( n - 1). La correlación parcial de orden cero ρ _{XY ·Ø} se define como el coeficiente de correlación regular ρ _XY .

Se cumple, para cualquier que ^[3] ${\displaystyle Z_{0}\in \mathbf {Z} ,}$

${\displaystyle \rho _{XY\cdot \mathbf {Z} }={\frac {\rho _{XY\cdot \mathbf {Z} \setminus \{Z_{0}\}}-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}}{{\sqrt {1-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}{\sqrt {1-\rho _{Z_{0}Y\cdot \mathbf {Z} \setminus \{Z_{0}\}}^{2}}}}}}$

Implementar este cálculo de manera ingenua como un algoritmo recursivo produce una complejidad temporal exponencial . Sin embargo, este cálculo tiene la propiedad de superposición de subproblemas , de modo que usar programación dinámica o simplemente almacenar en caché los resultados de las llamadas recursivas produce una complejidad de . ${\displaystyle {\mathcal {O}}(n^{3})}$

Nótese que en el caso en que Z es una sola variable, esto se reduce a: ^{[ cita requerida ]}

${\displaystyle \rho _{XY\cdot Z}={\frac {\rho _{XY}-\rho _{XZ}\rho _{ZY}}{{\sqrt {1-\rho _{XZ}^{2}}}{\sqrt {1-\rho _{ZY}^{2}}}}}}$

Utilizando la inversión de matrices

La correlación parcial también se puede escribir en términos de la matriz de precisión conjunta. Consideremos un conjunto de variables aleatorias, de cardinalidad n . Queremos la correlación parcial entre dos variables y dadas todas las demás, es decir, . Supongamos que la matriz de covarianza (conjunta/completa) es definida positiva y, por lo tanto, invertible . Si la matriz de precisión se define como , entonces ${\displaystyle \mathbf {V} ={X_{1},\dots ,X_{n}}}$ ${\displaystyle X_{i}}$ ${\displaystyle X_{j}}$ ${\displaystyle \mathbf {V} \setminus \{X_{i},X_{j}\}}$ ${\displaystyle \Sigma =(\sigma _{ij})}$ ${\displaystyle \Omega =(p_{ij})=\Sigma ^{-1}}$

Para calcular esto se requiere , la inversa de la matriz de covarianza que se ejecuta en el tiempo (utilizando la matriz de covarianza de muestra para obtener una correlación parcial de muestra). Tenga en cuenta que solo se requiere una única inversión de matriz para obtener todas las correlaciones parciales entre pares de variables en . ${\displaystyle \Sigma ^{-1}}$ ${\displaystyle \Sigma }$ ${\displaystyle {\mathcal {O}}(n^{3})}$ ${\displaystyle \mathbf {V} }$

Para demostrar la ecuación ( 1 ), regrese a la notación anterior (es decir , ) y comience con la definición de correlación parcial: ρ _{XY · Z} es la correlación entre los residuos e _X y e _Y resultantes de la regresión lineal de X con Z y de Y con Z , respectivamente. ${\displaystyle X,Y,\mathbf {Z} \leftrightarrow X_{i},X_{j},\mathbf {V} \setminus \{X_{i},X_{j}\}}$

En primer lugar, supongamos que son los coeficientes de ajuste de la regresión lineal; es decir, ${\displaystyle \beta ,\gamma }$

${\displaystyle \beta =\operatorname {argmin} _{\beta }\mathbb {E} \|X-\beta ^{T}Z\|^{2}}$

${\displaystyle \gamma =\operatorname {argmin} _{\gamma }\mathbb {E} \|Y-\gamma ^{T}Z\|^{2}}$

Escriba la matriz de covarianza conjunta para el vector como ${\displaystyle (X,Y,Z^{T})^{T}}$

${\displaystyle \Sigma ={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}&\Sigma _{XZ}\\\Sigma _{YX}&\Sigma _{YY}&\Sigma _{YZ}\\\Sigma _{ZX}&\Sigma _{ZY}&\Sigma _{ZZ}\end{bmatrix}}={\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\\\end{bmatrix}}}$

donde Entonces la fórmula estándar para la regresión lineal da $${\displaystyle C_{11}={\begin{bmatrix}\Sigma _{XX}&\Sigma _{XY}\\\Sigma _{YX}&\Sigma _{YY}\end{bmatrix}},\qquad C_{12}={\begin{bmatrix}\Sigma _{XZ}\\\Sigma _{YZ}\end{bmatrix}},\qquad C_{21}={\begin{bmatrix}\Sigma _{ZX}&\Sigma _{ZY}\end{bmatrix}},\qquad C_{22}=\Sigma _{ZZ}}$$

${\displaystyle \beta =\left(\Sigma _{ZZ}\right)^{-1}\Sigma _{ZX}}$

Por lo tanto, los residuos se pueden escribir como

${\displaystyle R_{X}=X-\beta ^{T}Z=X-\Sigma _{XZ}\left(\Sigma _{ZZ}\right)^{-1}Z}$

Tenga en cuenta que tiene una expectativa de cero debido a la inclusión de un término de intersección en . Calcular la covarianza ahora da ${\displaystyle R_{X}}$ ${\displaystyle Z}$

A continuación, escriba la matriz de precisión en una forma de bloque similar: ${\displaystyle \Omega =\Sigma ^{-1}}$

${\displaystyle \Omega ={\begin{bmatrix}\Omega _{XX}&\Omega _{XY}&\Omega _{XZ}\\\Omega _{YX}&\Omega _{YY}&\Omega _{YZ}\\\Omega _{ZX}&\Omega _{ZY}&\Omega _{ZZ}\end{bmatrix}}={\begin{bmatrix}P_{11}&P_{12}\\P_{21}&P_{22}\\\end{bmatrix}}}$

Luego, por la fórmula de Schur para la inversión de la matriz de bloques ,

${\displaystyle P_{11}^{-1}=C_{11}-C_{12}C_{22}^{-1}C_{21}}$

Las entradas de la matriz del lado derecho son precisamente las covarianzas calculadas previamente en ( 2 ), dando

${\displaystyle P_{11}^{-1}={\begin{bmatrix}\operatorname {Cov} (R_{X},R_{X})&\operatorname {Cov} (R_{X},R_{Y})\\\operatorname {Cov} (R_{Y},R_{X})&\operatorname {Cov} (R_{Y},R_{Y})\\\end{bmatrix}}}$

Usando la fórmula para la inversa de una matriz 2×2 se obtiene

${\displaystyle {\begin{aligned}P_{11}^{-1}&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}[P_{11}]_{22}&-[P_{11}]_{12}\\-[P_{11}]_{21}&[P_{11}]_{11}\\\end{pmatrix}}\\&={\frac {1}{{\text{det}}P_{11}}}{\begin{pmatrix}p_{YY}&-p_{XY}\\-p_{YX}&p_{XX}\\\end{pmatrix}}\end{aligned}}}$

De hecho, la correlación parcial es

${\displaystyle \rho _{XY\cdot Z}={\frac {\operatorname {Cov} (R_{X},R_{Y})}{\sqrt {\operatorname {Cov} (R_{X},R_{X})\operatorname {Cov} (R_{Y},R_{Y})}}}={\frac {-{\tfrac {1}{{\text{det}}P_{11}}}p_{XY}}{\sqrt {{\tfrac {1}{{\text{det}}P_{11}}}p_{XX}{\tfrac {1}{{\text{det}}P_{11}}}p_{YY}}}}=-{\frac {p_{XY}}{\sqrt {p_{XX}p_{YY}}}}}$

como se reivindica en ( 1 ).

Interpretación

Interpretación geométrica de la correlación parcial para el caso de N = 3 observaciones y, por tanto, un hiperplano bidimensional

Geométrico

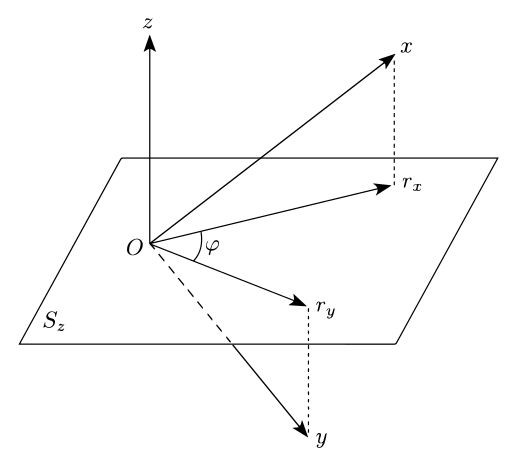
Sean tres variables X , Y , Z (donde Z es la variable "de control" o "extra") elegidas de una distribución de probabilidad conjunta sobre n variables V . Además, sean v _i , 1 ≤ i ≤ N , N observaciones iid n -dimensionales tomadas de la distribución de probabilidad conjunta sobre V . La interpretación geométrica proviene de considerar los vectores N -dimensionales x (formado por los valores sucesivos de X sobre las observaciones), y (formado por los valores de Y ), y z (formado por los valores de Z ).

Se puede demostrar que los residuos e _X,i provenientes de la regresión lineal de X sobre Z , si también se consideran como un vector N -dimensional e _X (denotado r _X en el gráfico adjunto), tienen un producto escalar cero con el vector z generado por Z . Esto significa que el vector de residuos se encuentra en un hiperplano ( N –1)-dimensional S _z que es perpendicular a z .

Lo mismo se aplica a los residuos e _Y,i que generan un vector e _Y . La correlación parcial deseada es entonces el coseno del ángulo φ entre las proyecciones e _X y e _Y de x e y , respectivamente, sobre el hiperplano perpendicular a z . ^{[4] : cap. 7}

Como prueba de independencia condicional

Suponiendo que todas las variables involucradas son gaussianas multivariadas , la correlación parcial ρ _{XY · Z} es cero si y solo si X es condicionalmente independiente de Y dado Z . ^[1] Esta propiedad no se cumple en el caso general.

Para comprobar si una correlación parcial de muestra implica que la correlación parcial de población real difiere de 0, se puede utilizar la transformada z de Fisher de la correlación parcial: ${\displaystyle {\hat {\rho }}_{XY\cdot \mathbf {Z} }}$

${\displaystyle z({\hat {\rho }}_{XY\cdot \mathbf {Z} })={\frac {1}{2}}\ln \left({\frac {1+{\hat {\rho }}_{XY\cdot \mathbf {Z} }}{1-{\hat {\rho }}_{XY\cdot \mathbf {Z} }}}\right)}$

La hipótesis nula es , que se probará frente a la alternativa de dos colas . puede rechazarse si ${\displaystyle H_{0}:\rho _{XY\cdot \mathbf {Z} }=0}$ ${\displaystyle H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0}$ ${\displaystyle H_{0}}$

${\displaystyle {\sqrt {N-|\mathbf {Z} |-3}}\cdot |z({\hat {\rho }}_{XY\cdot \mathbf {Z} })|>\Phi ^{-1}(1-\alpha /2)}$

donde es la función de distribución acumulada de una distribución gaussiana con media cero y desviación estándar unitaria , es el nivel de significancia de y es el tamaño de la muestra . Esta transformada z es aproximada y la distribución real del coeficiente de correlación (parcial) de la muestra no es sencilla. Sin embargo, está disponible una prueba t exacta basada en una combinación del coeficiente de regresión parcial, el coeficiente de correlación parcial y las varianzas parciales. ^[5] ${\displaystyle \Phi }$ ${\displaystyle \alpha }$ ${\displaystyle H_{0}}$ ${\displaystyle N}$

La distribución de la correlación parcial de la muestra fue descrita por Fisher. ^[6]

Correlación semiparcial (correlación parcial)

La estadística de correlación semiparcial (o parcial) es similar a la estadística de correlación parcial; ambas comparan variaciones de dos variables después de controlar ciertos factores. Sin embargo, para calcular la correlación semiparcial, se mantiene constante la tercera variable para X o Y, pero no para ambas; mientras que para la correlación parcial, se mantiene constante la tercera variable para ambas. ^[7] La ​​correlación semiparcial compara la variación única de una variable (habiendo eliminado la variación asociada con la (s) variable(s) Z ) con la variación sin filtrar de la otra, mientras que la correlación parcial compara la variación única de una variable con la variación única de la otra.

La correlación semiparcial puede considerarse más relevante en la práctica "porque está escalada a (es decir, en relación con) la variabilidad total en la variable dependiente (de respuesta)". ^[8] Por el contrario, es menos útil en teoría porque es menos precisa acerca del papel de la contribución única de la variable independiente.

El valor absoluto de la correlación semiparcial de X con Y es siempre menor o igual que el de la correlación parcial de X con Y . La razón es la siguiente: supongamos que la correlación de X con Z se ha eliminado de X , lo que da el vector residual e _x . Al calcular la correlación semiparcial, Y todavía contiene varianza única y varianza debida a su asociación con Z . Pero e _x , al no estar correlacionado con Z , solo puede explicar parte de la parte única de la varianza de Y y no la parte relacionada con Z . Por el contrario, con la correlación parcial, solo e _y (la parte de la varianza de Y que no está relacionada con Z ) debe explicarse, por lo que hay menos varianza del tipo que e _x no puede explicar.

Uso en análisis de series temporales

En el análisis de series de tiempo , la función de autocorrelación parcial (a veces "función de correlación parcial") de una serie de tiempo se define, para el rezago , como ^{[ cita requerida ]} ${\displaystyle h}$

${\displaystyle \varphi (h)=\rho _{X_{0}X_{h}\,\cdot \,\{X_{1},\,\dots \,,X_{h-1}\}}}$

Esta función se utiliza para determinar la longitud de retraso adecuada para una autorregresión .

Véase también

• Regresión lineal
• Independencia condicional
• Correlación múltiple
• Descomposición parcial de información

Referencias

1. Baba, Kunihiro; Ritei Shibata; Masaaki Sibuya (2004). "Correlación parcial y correlación condicional como medidas de independencia condicional". Revista de Estadística de Australia y Nueva Zelanda . 46 (4): 657–664. doi :10.1111/j.1467-842X.2004.00360.x. S2CID  123130024.
2. Guilford JP, Fruchter B. (1973). Estadísticas fundamentales en psicología y educación . Tokio: McGraw-Hill Kogakusha, LTD.
3. Kim, Seongho (noviembre de 2015). "ppcor: Un paquete R para un cálculo rápido de coeficientes de correlación semiparcial". Communications for Statistical Applications and Methods . 22 (6): 665–674. doi :10.5351/CSAM.2015.22.6.665. ISSN  2287-7843. PMC 4681537 . PMID  26688802. 
4. Rummel, RJ (1976). "Entendiendo la correlación".
5. Kendall MG, Stuart A. (1973) La teoría avanzada de la estadística , volumen 2 (3.ª edición), ISBN 0-85264-215-6 , sección 27.22 
6. Fisher, RA (1924). "La distribución del coeficiente de correlación parcial". Metron . 3 (3–4): 329–332.
7. "Correlación parcial y semiparcial". Archivado desde el original el 6 de febrero de 2014.
8. StatSoft, Inc. (2010). "Semi-Partial (or Part) Correlation", Electronic Statistics Textbook. Tulsa, OK: StatSoft, consultado el 15 de enero de 2011.

Enlaces externos

• Prokhorov, AV (2001) [1994], "Coeficiente de correlación parcial", Enciclopedia de Matemáticas , EMS Press
• Fórmulas matemáticas en la sección "Descripción" de la rutina PCORR de la biblioteca numérica IMSL
• Un ejemplo de tres variables