Complejidad del circuito

Modelo de complejidad computacional.

Ejemplo de circuito booleano. Los nodos son puertas Y , los nodos son puertas O y los nodos NO son puertas ${\displaystyle \wedge }$ ${\displaystyle \vee }$ ${\displaystyle \neg }$

En informática teórica , la complejidad de los circuitos es una rama de la teoría de la complejidad computacional en la que las funciones booleanas se clasifican según el tamaño o la profundidad de los circuitos booleanos que las calculan. Una noción relacionada es la complejidad del circuito de un lenguaje recursivo que se decide mediante una familia uniforme de circuitos (ver más abajo). ${\displaystyle C_{1},C_{2},\ldots }$

Demostrar límites inferiores en el tamaño de los circuitos booleanos que calculan funciones booleanas explícitas es un enfoque popular para separar clases de complejidad. Por ejemplo, una clase de circuito prominente P/poly consta de funciones booleanas computables mediante circuitos de tamaño polinómico. Demostrar eso separaría P y NP (ver más abajo). ${\displaystyle {\mathsf {NP}}\not \subseteq {\mathsf {P/poly}}}$

Las clases de complejidad definidas en términos de circuitos booleanos incluyen AC 0 , AC , TC 0 , NC 1 , NC y P/poly .

Tamaño y profundidad

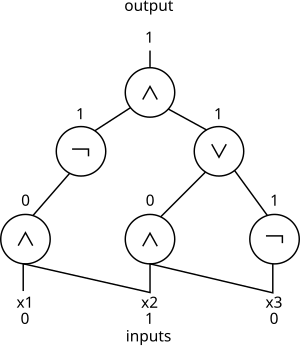
Un circuito booleano con bits de entrada es un gráfico acíclico dirigido en el que cada nodo (generalmente llamado puertas en este contexto) es un nodo de entrada de grado 0 etiquetado por uno de los bits de entrada, una puerta AND , una puerta OR , o una puerta NO . Una de estas puertas se designa como puerta de salida. Un circuito de este tipo calcula naturalmente una función de sus entradas. El tamaño de un circuito es el número de puertas que contiene y su profundidad es la longitud máxima de un camino desde una puerta de entrada hasta la puerta de salida. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Hay dos nociones principales de complejidad de circuito ^[1] La complejidad del tamaño del circuito de una función booleana es el tamaño mínimo de cualquier cálculo de circuito . La complejidad de la profundidad del circuito de una función booleana es la profundidad mínima de cualquier cálculo de circuito . ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f}$

Estas nociones se generalizan cuando se considera la complejidad del circuito de cualquier lenguaje que contenga cadenas con diferentes longitudes de bits, especialmente los lenguajes formales infinitos . Los circuitos booleanos, sin embargo, sólo permiten un número fijo de bits de entrada. Por tanto, ningún circuito booleano es capaz de decidir dicho lenguaje. Para tener en cuenta esta posibilidad, se consideran familias de circuitos donde cada uno acepta entradas de tamaño . Cada familia de circuitos generará naturalmente el lenguaje mediante la salida del circuito cuando una cadena de longitud sea miembro de la familia, y en caso contrario. Decimos que una familia de circuitos es de tamaño mínimo si no hay otra familia que decida sobre entradas de cualquier tamaño, con un circuito de tamaño menor que (respectivamente para familias de mínimos de profundidad ). Por tanto, la complejidad del circuito es significativa incluso para lenguajes no recursivos . La noción de familia uniforme permite relacionar variantes de complejidad de circuitos con medidas de complejidad basadas en algoritmos de lenguajes recursivos. Sin embargo, la variante no uniforme es útil para encontrar límites inferiores de cuán compleja debe ser cualquier familia de circuitos para decidir idiomas determinados. ${\displaystyle C_{1},C_{2},\ldots }$ ${\displaystyle C_{n}}$ ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle 1}$ ${\displaystyle n}$ ${\displaystyle 0}$ ${\displaystyle n}$ ${\displaystyle C_{n}}$

Por lo tanto, la complejidad del tamaño del circuito de un lenguaje formal se define como la función que relaciona la longitud de un bit de una entrada, con la complejidad del tamaño del circuito de un circuito mínimo que decide si las entradas de esa longitud están en . La complejidad de la profundidad del circuito se define de manera similar. ${\displaystyle A}$ ${\displaystyle t:\mathbb {N} \to \mathbb {N} }$ ${\displaystyle n}$ ${\displaystyle C_{n}}$ ${\displaystyle A}$

Uniformidad

Los circuitos booleanos son uno de los principales ejemplos de los llamados modelos de cálculo no uniformes , en el sentido de que entradas de diferentes longitudes son procesadas por diferentes circuitos, en contraste con modelos uniformes como las máquinas de Turing , donde se utiliza el mismo dispositivo computacional para todos. posibles longitudes de entrada. Por lo tanto, un problema computacional individual está asociado con una familia particular de circuitos booleanos donde cada uno es el circuito que maneja entradas de n bits. A menudo se impone una condición de uniformidad a estas familias, lo que requiere la existencia de alguna máquina de Turing posiblemente limitada por recursos que, con la entrada n , produzca una descripción del circuito individual . Cuando esta máquina de Turing tiene un polinomio de tiempo de ejecución en n , se dice que la familia de circuitos es P-uniforme. El requisito más estricto de uniformidad DLOGTIME es de particular interés en el estudio de clases de circuitos de poca profundidad como AC ⁰ o TC ⁰ . Cuando no se especifican límites de recursos, un lenguaje es recursivo (es decir, decidible por una máquina de Turing) si y sólo si el lenguaje es decidido por una familia uniforme de circuitos booleanos. ${\displaystyle C_{1},C_{2},\dots }$ ${\displaystyle C_{n}}$ ${\displaystyle C_{n}}$

Uniforme de tiempo polinomial

Una familia de circuitos booleanos es uniforme en tiempo polinomial si existe una máquina de Turing determinista M , tal que ${\displaystyle \{C_{n}:n\in \mathbb {N} \}}$

• M se ejecuta en tiempo polinomial
• Para todos , M genera una descripción de la entrada ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle C_{n}}$ ${\displaystyle 1^{n}}$

Uniforme del espacio de registro

Una familia de circuitos booleanos es uniforme en el espacio logarítmico si existe una máquina de Turing determinista M , tal que ${\displaystyle \{C_{n}:n\in \mathbb {N} \}}$

• M se ejecuta en un espacio de trabajo logarítmico (es decir, M es un transductor de espacio logarítmico )
• Para todos , M genera una descripción de la entrada ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle C_{n}}$ ${\displaystyle 1^{n}}$

Historia

La complejidad de los circuitos se remonta a Shannon en 1949, ^[2] quien demostró que casi todas las funciones booleanas en n variables requieren circuitos de tamaño Θ(2 ⁿ / n ). A pesar de este hecho, los teóricos de la complejidad hasta ahora no han podido demostrar un límite inferior superlineal para ninguna función explícita.

Los límites inferiores de los superpolinomios se han demostrado bajo ciertas restricciones en la familia de circuitos utilizados. La primera función para la cual se mostraron los límites inferiores del circuito superpolinomial fue la función de paridad , que calcula la suma de sus bits de entrada módulo 2. El hecho de que la paridad no esté contenida en AC 0 fue establecido por primera vez de forma independiente por Ajtai en 1983 ^{[3] [4 ]} y por Furst, Saxe y Sipser en 1984. ^[5] Mejoras posteriores realizadas por Håstad en 1987 ^[6] establecieron que cualquier familia de circuitos de profundidad constante que calculen la función de paridad requiere un tamaño exponencial. Ampliando un resultado de Razborov, ^[7] Smolensky en 1987 ^[8] demostró que esto es cierto incluso si el circuito se aumenta con puertas que calculan la suma de sus bits de entrada módulo algún primo impar p .

El problema de k -clique es decidir si un gráfico dado en n vértices tiene un clique de tamaño k . Para cualquier elección particular de las constantes n y k , el gráfico se puede codificar en binario usando bits, que indican para cada borde posible si está presente. Luego, el problema de k -clique se formaliza como una función tal que genera 1 si y solo si el gráfico codificado por la cadena contiene un clique de tamaño k . Esta familia de funciones es monótona y puede calcularse mediante una familia de circuitos, pero se ha demostrado que no puede calcularse mediante una familia de circuitos monótonos de tamaño polinómico (es decir, circuitos con puertas Y y O pero sin negación). El resultado original de Razborov en 1985 ^[7] fue posteriormente mejorado a un límite inferior de tamaño exponencial por Alon y Boppana en 1987. ^[9] En 2008, Rossman ^[10] demostró que los circuitos de profundidad constante con AND, OR y NOT las puertas requieren tamaño para resolver el problema de k -clique incluso en el caso promedio . Además, existe un circuito de tamaño que calcula . ${\displaystyle {n \choose 2}}$ ${\displaystyle f_{k}:\{0,1\}^{n \choose 2}\to \{0,1\}}$ ${\displaystyle f_{k}}$ ${\displaystyle \Omega (n^{k/4})}$ ${\displaystyle n^{k/4+O(1)}}$ ${\displaystyle f_{k}}$

En 1999, Raz y McKenzie demostraron más tarde que la jerarquía NC monótona es infinita. ^[11]

El problema de la división de enteros radica en TC 0 uniforme . ^[12]

Límites inferiores del circuito

Los límites inferiores del circuito son generalmente difíciles. Los resultados conocidos incluyen

• La paridad no se da en AC 0 no uniforme , como lo demostraron Ajtai en 1983 ^{[3] [4]} , así como Furst, Saxe y Sipser en 1984. ^[5]
• El TC ⁰ uniforme está estrictamente contenido en PP , como lo demuestra Allender. ^[13]
• las clases sP 2, PP ^{[nb 1]} y MA /1 ^[14] (MA con un pequeño consejo) no están en TAMAÑO ( n ^k ) para ninguna constante k.
• Si bien se sospecha que la clase no uniforme ACC ⁰ no contiene la función mayoritaria, no fue hasta 2010 que Williams lo demostró . ^[15] ${\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {ACC}}^{0}}$

Está abierto si NEXPTIME tiene circuitos TC ⁰ no uniformes .

Las pruebas de los límites inferiores del circuito están fuertemente relacionadas con la desrandomización . Una prueba que implicaría que cualquiera de los permanentes no puede calcularse mediante circuitos aritméticos no uniformes (polinomios) de tamaño y grado polinomiales. ^[dieciséis] ${\displaystyle {\mathsf {P}}={\mathsf {BPP}}}$ ${\displaystyle {\mathsf {NEXP}}\not \subseteq {\mathsf {P/poly}}}$

En 1997, Razborov y Rudich demostraron que muchos límites inferiores de circuitos conocidos para funciones booleanas explícitas implican la existencia de las llamadas propiedades naturales útiles frente a la clase de circuito respectiva. ^[17] Por otro lado, las propiedades naturales útiles contra P/poly romperían fuertes generadores pseudoaleatorios. Esto a menudo se interpreta como una barrera de "pruebas naturales" para demostrar límites inferiores de circuito fuertes. En 2016, Carmosino, Impagliazzo, Kabanets y Kolokolova demostraron que las propiedades naturales también se pueden utilizar para construir algoritmos de aprendizaje eficientes. ^[18]

Clases de complejidad

Muchas clases de complejidad de circuitos se definen en términos de jerarquías de clases. Para cada entero no negativo i , hay una clase NC i , que consta de circuitos de tamaño polinomial de profundidad , que utilizan puertas AND, OR y NOT de entrada en abanico acotadas. La unión NC de todas estas clases es un tema de discusión. Al considerar puertas de entrada en abanico ilimitadas, se pueden construir las clases AC i y AC (que es igual a NC). Se pueden construir muchas otras clases de complejidad de circuitos con el mismo tamaño y restricciones de profundidad permitiendo diferentes conjuntos de puertas. ${\displaystyle O(\log ^{i}(n))}$

Relación con la complejidad del tiempo

Si un determinado lenguaje pertenece a la clase de complejidad temporal para alguna función , entonces tiene complejidad de circuito . Si la máquina de Turing que acepta el lenguaje no se da cuenta (lo que significa que lee y escribe las mismas celdas de memoria independientemente de la entrada), entonces tiene complejidad de circuito . ^[19] ${\displaystyle A}$ ${\displaystyle {\text{TIME}}(t(n))}$ ${\displaystyle t:\mathbb {N} \to \mathbb {N} }$ ${\displaystyle A}$ ${\displaystyle {\mathcal {O}}(t(n)\log t(n))}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {O}}(t(n))}$

circuitos monótonos

Un circuito booleano monótono es aquel que tiene sólo puertas AND y OR, pero ninguna puerta NOT. Un circuito monótono solo puede calcular una función booleana monótona, que es una función donde para cada , donde significa que para todos . ${\displaystyle f:\{0,1\}^{n}\to \{0,1\}}$ ${\displaystyle x,y\in \{0,1\}^{n}}$ ${\displaystyle x\leq y\implies f(x)\leq f(y)}$ ${\displaystyle x\leq y}$ ${\displaystyle x_{i}\leq y_{i}}$ ${\displaystyle i\in \{1,\ldots ,n\}}$

Ver también

• Minimización de circuitos

Notas

1. Ver prueba .

Referencias

1. Sipser, Michael (1997). Introducción a la teoría de la computación (1 ed.). Boston, Estados Unidos: Compañía editorial PWS. pag. 324.
2. Shannon, Claude Elwood (1949). "La síntesis de circuitos de conmutación de dos terminales". Revista técnica del sistema Bell . 28 (1): 59–98. doi :10.1002/j.1538-7305.1949.tb03624.x.
3. Ajtai, Miklós (1983). " -fórmulas sobre estructuras finitas". Anales de lógica pura y aplicada . 24 : 1–24. doi :10.1016/0168-0072(83)90038-6. ${\displaystyle \Sigma _{1}^{1}}$
4. Ajtai, Miklós ; Komlós, János ; Szemerédi, Endre (1983). "Una red de clasificación". Actas del 15º Simposio Anual de la ACM sobre Teoría de la Computación, 25 al 27 de abril de 1983, Boston, Massachusetts, EE. UU . Asociación para Maquinaria de Computación. págs. 1–9. doi :10.1145/800061.808726. ${\displaystyle O(n\log n)}$
5. Furst, Merrick L.; Sajonia, James Benjamín ; Sipser, Michael Fredric (1984). "Paridad, circuitos y jerarquía de tiempo polinomial". Teoría de Sistemas Matemáticos . 17 (1): 13–27. doi :10.1007/BF01744431. SEÑOR  0738749. S2CID  6306235.
6. Håstad, Johan Torkel (1987). Limitaciones computacionales de circuitos de pequeña profundidad (PDF) (tesis doctoral). Instituto de Tecnología de Massachusetts.
7. Razborov, Aleksandr Aleksandrovich (1985). "Límites inferiores de la complejidad monótona de algunas funciones booleanas". Matemáticas soviéticas - Doklady . 31 : 354–357. ISSN  0197-6788.
8. Smolensky, romano (1987). "Métodos algebraicos en la teoría de límites inferiores para la complejidad de circuitos booleanos". Actas del 19º Simposio Anual ACM sobre Teoría de la Computación . Asociación para Maquinaria de Computación . págs. 77–82. doi : 10.1145/28395.28404 .
9. Alón, Noga ; Boppana, Ravi B. (1987). "La complejidad del circuito monótono de las funciones booleanas". Combinatoria . 7 (1): 1–22. CiteSeerX 10.1.1.300.9623 . doi :10.1007/bf02579196. S2CID  17397273. 
10. Rossman, Benjamín E. (2008). "Sobre la complejidad constante de k-clique". STOC 2008: Actas del 40º simposio anual de ACM sobre teoría de la informática . Asociación para Maquinaria de Computación . págs. 721–730. doi :10.1145/1374376.1374480.
11. Raz, corrió ; McKenzie, Pierre (1999). "Separación de la jerarquía NC monótona". Combinatoria . 19 (3): 403–435. doi :10.1007/s004930050062.
12. Hesse, William (2001). "La división está en uniforme TC ⁰ ". Actas del 28º Coloquio Internacional sobre Autómatas, Lenguajes y Programación . Springer Verlag . págs. 104-114.
13. Allender, Eric (1996). "Complejidad del circuito antes del amanecer del nuevo milenio". En Chandru, Vijay; Vinay, V. (eds.). Fundamentos de la tecnología del software y la informática teórica, 16.ª conferencia, Hyderabad, India, 18 al 20 de diciembre de 1996, Actas . Apuntes de conferencias sobre informática. vol. 1180. Saltador. págs. 1–18. doi :10.1007/3-540-62034-6_33.
14. Santhanam, Rahul (2007). "Límites inferiores del circuito para clases de Merlin-Arthur". STOC 2007: Actas del trigésimo noveno simposio anual de ACM sobre teoría de la informática . págs. 275–283. CiteSeerX 10.1.1.92.4422 . doi :10.1145/1250790.1250832. 
15. Williams, Richard Ryan (2011). "Límites inferiores del circuito ACC no uniforme" (PDF) . CCC 2011: Actas de la 26ª Conferencia Anual del IEEE sobre Complejidad Computacional . págs. 115-125. doi :10.1109/CCC.2011.36.
16. Kabanets, San Valentín; Impagliazzo, Russell Graham (2004). "Desaleatorizar las pruebas de identidad polinómica significa probar los límites inferiores del circuito". Complejidad computacional . 13 (1): 1–46. doi :10.1007/s00037-004-0182-6. S2CID  12451799.
17. Razborov, Aleksandr Aleksandrovich ; Rüdich, Steven (1997). "Pruebas naturales". Revista de Ciencias de la Computación y de Sistemas . vol. 55, págs. 24-35.
18. Carmosino, Marco; Impagliazzo, Russell Graham ; Kabanets, Valentín; Kolokolova, Antonina (2016). "Aprendizaje de algoritmos a partir de pruebas naturales". Jornada de Complejidad Computacional .
19. Pippenger, Nicolás ; Fischer, Michael J. (1979). "Relaciones entre medidas de complejidad". Revista de la ACM . 26 (3): 361–381. doi : 10.1145/322123.322138 . S2CID  2432526.

Otras lecturas

• Vollmer, Heribert [en alemán] (1999). Introducción a la complejidad de los circuitos: un enfoque uniforme . Textos de Informática Teórica. Una serie EATCS. Springer Verlag . ISBN 978-3-540-64310-4.
• Wegener, Ingo (1987) [noviembre de 1986]. La complejidad de las funciones booleanas . Serie Wiley-Teubner en Ciencias de la Computación. Frankfurt am Main/Bielefeld, Alemania: John Wiley & Sons Ltd. y BG Teubner Verlag , Stuttgart. ISBN 3-519-02107-2. LCCN  87-10388.(xii+457 páginas) (NB. En ese momento, un libro de texto influyente sobre el tema, comúnmente conocido como el "Libro Azul". También disponible para descargar (PDF) en el Coloquio Electrónico sobre Complejidad Computacional .)
• Zwick, Uri . "Apuntes de un curso de Uri Zwick sobre complejidad de circuitos".