En teoría de grafos , los ciclos cúbicos conexos son grafos cúbicos no dirigidos , formados al reemplazar cada vértice de un grafo hipercubico por un ciclo . Fue introducido por Preparata y Vuillemin (1981) para su uso como topología de red en computación paralela .
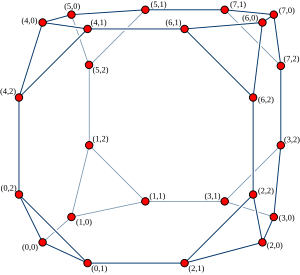
Los ciclos cúbicos conexos de orden n (denotados como CCC n ) se pueden definir como un grafo formado a partir de un conjunto de n 2 n nodos, indexados por pares de números ( x , y ) donde 0 ≤ x < 2 n y 0 ≤ y < n . Cada uno de estos nodos está conectado a tres vecinos: ( x , ( y + 1) mod n ) , ( x , ( y − 1) mod n ) y ( x ⊕ 2 y , y ) , donde "⊕" denota la operación exclusiva bit a bit o sobre números binarios.
Este gráfico también puede interpretarse como el resultado de reemplazar cada vértice de un gráfico hipercubo de n dimensiones por un ciclo de n vértices. Los vértices del gráfico hipercubo están indexados por los números x y las posiciones dentro de cada ciclo por los números y .
Los ciclos cúbicos conexos de orden n son el gráfico de Cayley de un grupo que actúa sobre palabras binarias de longitud n mediante rotación e inversión de bits de la palabra. [1] Los generadores utilizados para formar este gráfico de Cayley a partir del grupo son los elementos del grupo que actúan rotando la palabra una posición a la izquierda, rotándola una posición a la derecha o invirtiendo su primer bit. Debido a que es un gráfico de Cayley, es transitivo de vértice : existe una simetría del gráfico que asigna cualquier vértice a cualquier otro vértice.
El diámetro de los ciclos conexos al cubo de orden n es 2 n + ⌊n/2⌋ − 2 para cualquier n ≥ 4; el punto más alejado de ( x , y ) es (2 n − x − 1, ( y + n /2) mod n ). [2] Sýkora y Vrťo (1993) demostraron que el número de cruces de CCC n es ((1/20) + o(1)) 4 n .
Según la conjetura de Lovász , el gráfico de ciclo conexo al cubo siempre debería contener un ciclo hamiltoniano , y ahora se sabe que esto es cierto. En términos más generales, aunque estos gráficos no son pancíclicos , contienen ciclos de todas las longitudes pares posibles, excepto un número acotado, y cuando n es impar, también contienen muchas de las longitudes impares posibles de los ciclos. [3]
Preparata y Vuillemin (1981) investigaron los ciclos conexos en cubos y aplicaron estos gráficos como patrón de interconexión de una red que conecta los procesadores en una computadora paralela . En esta aplicación, los ciclos conexos en cubos tienen las ventajas de conectividad de los hipercubos, pero solo requieren tres conexiones por procesador. Preparata y Vuillemin demostraron que un diseño plano basado en esta red tiene una complejidad óptima de área × tiempo 2 para muchas tareas de procesamiento en paralelo.