La computación inversa es una aplicación de software del concepto de computación reversible .
La computación reversible se ha estudiado ampliamente en el área de la arquitectura informática porque ofrece una posible solución al problema del calor al que se enfrentan los fabricantes de chips. La promesa de la computación reversible es que la cantidad de pérdida de calor para arquitecturas reversibles sería mínima para cantidades significativamente grandes de transistores. [1] [2] En lugar de crear entropía (y, por lo tanto, calor) mediante operaciones destructivas, una arquitectura reversible conserva la energía realizando otras operaciones que preservan el estado del sistema. [3] [4]
El concepto de computación inversa es algo más simple que la computación reversible, ya que la computación inversa solo se requiere para restaurar el estado equivalente de una aplicación de software, en lugar de respaldar la reversibilidad del conjunto de todas las instrucciones posibles. Los conceptos de computación reversible se han aplicado con éxito como computación inversa en áreas de aplicaciones de software como diseño de bases de datos, [5] puntos de control y depuración, [6] y diferenciación de código. [7] [8]
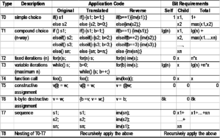
Basándose en la aplicación exitosa de los conceptos de computación inversa en otros dominios de software, Chris Carothers, Kalyan Perumalla y Richard Fujimoto [9] sugieren la aplicación de computación inversa para reducir los costos de ahorro de estado en la simulación de eventos discretos en paralelo (PDES). Definen un enfoque basado en códigos de eventos inversos (que se pueden generar automáticamente) y demuestran las ventajas de rendimiento de este enfoque sobre el ahorro de estado tradicional para aplicaciones de grano fino (aquellas con una pequeña cantidad de computación por evento). La propiedad clave que explota la computación inversa es que la mayoría de las operaciones que modifican las variables de estado son de naturaleza "constructiva". Es decir, la operación de deshacer para tales operaciones no requiere historial. Solo se requieren los valores más actuales de las variables para deshacer la operación. Por ejemplo, operadores como ++, ––, +=, -=, *= y /= pertenecen a esta categoría. Tenga en cuenta que los operadores *= y /= requieren un tratamiento especial en el caso de multiplicación o división por cero y condiciones de desbordamiento/subdesbordamiento. Aquí también pertenecen operaciones más complejas, como el desplazamiento circular (siendo el intercambio un caso especial) y ciertas clases de generación de números aleatorios .
Las operaciones de la forma a = b, cálculos módulo y bit a bit que resultan en la pérdida de datos, se denominan destructivas. Por lo general, estas operaciones solo se pueden restaurar utilizando técnicas convencionales de recuperación de estado. Sin embargo, observamos que muchas de estas operaciones destructivas son una consecuencia de la llegada de datos contenidos en el evento que se está procesando. Por ejemplo, en el trabajo de Yaun, Carothers, et al., con simulación TCP a gran escala, [10] la hora del último envío registra la marca de tiempo del último paquete reenviado en un proceso lógico de enrutador. La operación de intercambio hace que esta operación sea reversible.

En 1985, Jefferson introdujo el protocolo de sincronización optimista, que se utilizó en simulaciones de eventos discretos paralelos, conocido como Time Warp. [11] Hasta la fecha, la técnica conocida como Computación Inversa solo se ha aplicado en software para simulación de eventos discretos paralelos y sincronizados de manera optimista.
En diciembre de 1999, Michael Frank se graduó en la Universidad de Florida . Su tesis doctoral se centró en la computación inversa a nivel de hardware, pero incluyó descripciones tanto de una arquitectura de conjunto de instrucciones como de un lenguaje de programación de alto nivel (R) para un procesador basado en computación inversa. [12] [notas 1]
En 1998, Carothers y Perumalla publicaron un artículo para el taller Principles of Advanced and Distributed Simulation [13] como parte de sus estudios de posgrado con Richard Fujimoto, introduciendo la técnica de Computación Inversa como un mecanismo alternativo de reversión en simulaciones de eventos discretos paralelos sincronizados de manera optimista (Time Warp). En 1998, Carothers se convirtió en profesor asociado en el Instituto Politécnico Rensselaer . Trabajando con los estudiantes de posgrado David Bauer y Shawn Pearce, Carothers integró el diseño de Georgia Tech Time Warp en el Sistema de Simulación Optimista (ROSS) de Rensselaer, que solo admitía computación inversa como mecanismo de reversión. Carothers también construyó modelos RC para BitTorrent en General Electric, así como numerosos protocolos de red con estudiantes ( BGP4 , TCP Tahoe, Multicast ). Carothers creó un curso sobre Simulación Paralela y Distribuida en el que se requería que los estudiantes construyeran modelos RC en ROSS.
Casi al mismo tiempo, Perumalla se graduó de Georgia Tech y fue a trabajar al Laboratorio Nacional Oak Ridge (ORNL). Allí construyó el simulador uSik, que era un PDES de protocolo optimista/conservador combinado. El sistema era capaz de determinar dinámicamente el mejor protocolo para los LP y reasignarlos durante la ejecución en respuesta a la dinámica del modelo. En 2007, Perumalla probó uSik en Blue Gene/L y descubrió que, si bien la escalabilidad está limitada a procesadores de 8K para la implementación de Time Warp pura, la implementación conservadora escala a 16K procesadores disponibles. Tenga en cuenta que la evaluación comparativa se realizó utilizando PHOLD con una tasa de eventos remotos restringida del 10%, donde la marca de tiempo de los eventos se determinó mediante una distribución exponencial con una media de 1.0 y un lookahead adicional de 1.0 agregado a cada evento. Esta fue la primera implementación de PDES en Blue Gene utilizando computación inversa.
De 1998 a 2005, Bauer realizó un trabajo de posgrado en RPI bajo la dirección de Carothers, centrándose únicamente en la computación inversa. Desarrolló el primer sistema PDES basado únicamente en computación inversa, llamado Sistema de Simulación Optimista de Rensselaer (ROSS). [14] para sistemas combinados de memoria compartida y distribuida . De 2006 a 2009, Bauer trabajó bajo la dirección de EH Page en Mitre Corporation y, en colaboración con Carothers y Pearce, llevó el simulador ROSS al procesador 131.072 Blue Gene/P (Intrepid). Esta implementación fue estable para tasas de eventos remotos del 100 % (cada evento enviado a través de la red). Durante su tiempo en RPI y MITRE, Bauer desarrolló el sistema de simulación de red ROSS.Net [15] que admite el diseño de experimentos semiautomatizados para la optimización de caja negra de modelos de protocolo de red que se ejecutan en ROSS. Un objetivo principal del sistema era optimizar múltiples modelos de protocolo de red para su ejecución en ROSS. Por ejemplo, la creación de una estructura de capas de LP para eliminar los eventos que se transmiten entre los LP de protocolo de red en la misma máquina simulada optimiza la simulación de los nodos de red TCP/IP al eliminar las marcas de tiempo de desplazamiento cero entre los protocolos TCP e IP. Bauer también construyó modelos basados en agentes RC para redes de contacto social para estudiar los efectos de las enfermedades infecciosas , en particular la gripe pandémica, que se escalan a cientos de millones de agentes; así como modelos RC para redes ad-hoc móviles que implementan la funcionalidad de movilidad (detección de proximidad) y propagación de ondas electromagnéticas de capa física de alta precisión (modelo de matriz de línea de transmisión). [16]
Recientemente, la comunidad PDES también ha dado un impulso al ámbito de la simulación continua. Por ejemplo, Fujimoto y Perumalla, en colaboración con Tang et al. [17], han implementado un modelo RC de partícula en célula y han demostrado una excelente aceleración con respecto a la simulación continua para modelos de luz como partícula. Bauer y Page demostraron una excelente aceleración para un modelo RC de matriz de línea de transmisión (PB Johns, 1971), que modela la luz como una onda a frecuencias de microondas. Bauer también creó una variante RC de SEIR que genera una enorme mejora con respecto a los modelos continuos en el área de propagación de enfermedades infecciosas. Además, el modelo RC SEIR es capaz de modelar múltiples enfermedades de manera eficiente, mientras que el modelo continuo explota exponencialmente con respecto al número de combinaciones de enfermedades posibles en toda la población.
{{cite book}}: |journal=ignorado ( ayuda )