En la teoría de autómatas , una rama de la informática teórica , un ω -autómata (o autómata de flujo ) es una variación de un autómata finito que se ejecuta en cadenas infinitas, en lugar de finitas, como entrada. Dado que los ω-autómatas no se detienen, tienen una variedad de condiciones de aceptación en lugar de simplemente un conjunto de estados de aceptación.
Los ω-autómatas son útiles para especificar el comportamiento de sistemas que no se espera que terminen, como hardware, sistemas operativos y sistemas de control . Para tales sistemas, uno puede querer especificar una propiedad como "para cada solicitud, eventualmente sigue un reconocimiento", o su negación "hay una solicitud que no es seguida por un reconocimiento". La primera es una propiedad de palabras infinitas: no se puede decir de una secuencia finita que satisface esta propiedad.
Las clases de ω-autómatas incluyen los autómatas de Büchi , los autómatas de Rabin, los autómatas de Streett, los autómatas de paridad y los autómatas de Muller , cada uno de ellos determinista o no determinista. Estas clases de ω-autómatas difieren solo en términos de condición de aceptación. Todos ellos reconocen con precisión los ω-lenguajes regulares excepto el autómata determinista de Büchi, que es estrictamente más débil que todos los demás. Aunque todos estos tipos de autómatas reconocen el mismo conjunto de ω-lenguajes , no obstante difieren en la concisión de la representación para un ω-lenguaje dado.
Formalmente, un ω-autómata determinista es una tupla A = ( Q ,Σ,δ, Q 0 , Acc ) que consta de los siguientes componentes:
Una entrada para A es una cadena infinita sobre el alfabeto Σ, es decir, es una secuencia infinita α = ( a 1 , a 2 , a 3 ,...). La ejecución de A en dicha entrada es una secuencia infinita ρ = ( r 0 , r 1 , r 2 ,...) de estados, definida de la siguiente manera:
El propósito principal de un ω-autómata es definir un subconjunto del conjunto de todas las entradas: el conjunto de entradas aceptadas . Mientras que en el caso de un autómata finito ordinario cada ejecución termina con un estado r n y la entrada se acepta si y solo si r n es un estado de aceptación, la definición del conjunto de entradas aceptadas es más complicada para los ω-autómatas. Aquí debemos observar la ejecución completa ρ. La entrada se acepta si la ejecución correspondiente está en Acc . El conjunto de ω-palabras de entrada aceptadas se denomina ω-lenguaje reconocido por el autómata, que se denota como L(A).
La definición de Acc como subconjunto de Q ω es puramente formal y no es adecuada para la práctica porque normalmente dichos conjuntos son infinitos. La diferencia entre los distintos tipos de ω-autómatas (Büchi, Rabin, etc.) consiste en cómo codifican determinados subconjuntos Acc de Q ω como conjuntos finitos y, por tanto, en qué subconjuntos pueden codificar.
Formalmente, un ω-autómata no determinista es una tupla A = ( Q ,Σ,Δ, Q 0 , Acc ) que consta de los siguientes componentes:
A diferencia de un ω-autómata determinista, que tiene una función de transición δ, la versión no determinista tiene una relación de transición Δ. Nótese que Δ puede considerarse como una función: Q × Σ → P ( Q ) de Q × Σ al conjunto potencia P ( Q ). Por lo tanto, dado un estado q n y un símbolo a n , el siguiente estado q n +1 no está necesariamente determinado de forma única, sino que hay un conjunto de posibles siguientes estados.
Una ejecución de A en la entrada α = ( a 1 , a 2 , a 3 ,...) es cualquier secuencia infinita ρ = ( r 0 , r 1 , r 2 ,...) de estados que satisface las siguientes condiciones:
Un ω-autómata no determinista puede admitir muchas ejecuciones diferentes en cualquier entrada dada, o ninguna en absoluto. La entrada es aceptada si al menos una de las ejecuciones posibles es aceptable. El hecho de que una ejecución sea aceptable depende únicamente de Acc , como en el caso de los ω-autómatas deterministas. Todo ω-autómata determinista puede considerarse un ω-autómata no determinista tomando Δ como el gráfico de δ. Las definiciones de ejecuciones y aceptación para los ω-autómatas deterministas son, por tanto, casos especiales de los casos no deterministas.
Las condiciones de aceptación pueden ser conjuntos infinitos de palabras ω. Sin embargo, la mayoría de las personas estudian condiciones de aceptación que son finitamente representables. A continuación se enumeran diversas condiciones de aceptación populares.
Antes de analizar la lista, hagamos la siguiente observación. En el caso de sistemas que se ejecutan infinitamente, a menudo nos interesa saber si un determinado comportamiento se repite infinitamente a menudo. Por ejemplo, si una tarjeta de red recibe infinitas solicitudes de ping, es posible que no responda a algunas de ellas, pero debería responder a un subconjunto infinito de solicitudes de ping recibidas. Esto motiva la siguiente definición: para cualquier ejecución ρ, sea Inf(ρ) el conjunto de estados que se producen infinitamente a menudo en ρ. Esta noción de que ciertos estados se visitan infinitamente a menudo será útil para definir las siguientes condiciones de aceptación.
Todo autómata de Büchi puede considerarse un autómata de Müller. Basta con sustituir F por F ', que está constituido por todos los subconjuntos de Q que contienen al menos un elemento de F. De manera similar, todo autómata de Rabin, Streett o de paridad también puede considerarse un autómata de Müller.
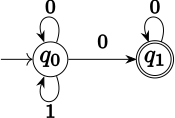
El siguiente lenguaje ω L sobre el alfabeto Σ = {0,1}, que puede ser reconocido por un autómata Büchi no determinista: L consiste en todas las ω-palabras en Σ ω en las que 1 aparece solo un número finito de veces. Un autómata Büchi no determinista que reconoce L necesita solo dos estados q 0 (el estado inicial) y q 1 . Δ consiste en los triples ( q 0 ,0, q 0 ), ( q 0 ,1, q 0 ), ( q 0 ,0, q 1 ) y ( q 1 ,0, q 1 ). F = { q 1 }. Para cualquier entrada α en la que 1 aparece solo un número finito de veces, hay una ejecución que permanece en el estado q 0 mientras haya 1 para leer, y pasa al estado q 1 después. Esta ejecución es exitosa. Si hay infinitos 1, entonces solo hay una ejecución posible: la que siempre permanece en el estado q 0 . (Una vez que la máquina ha salido de q 0 y ha llegado a q 1 , no puede regresar. Si se lee otro 1, no hay estado sucesor).
Obsérvese que el lenguaje anterior no puede ser reconocido por un autómata Büchi determinista , que es estrictamente menos expresivo que su contraparte no determinista.
Un ω-lenguaje sobre un alfabeto finito Σ es un conjunto de ω-palabras sobre Σ, es decir, es un subconjunto de Σ ω . Se dice que un ω-lenguaje sobre Σ es reconocido por un ω-autómata A (con el mismo alfabeto) si es el conjunto de todas las ω-palabras aceptadas por A . El poder expresivo de una clase de ω-autómatas se mide por la clase de todos los ω-lenguajes que pueden ser reconocidos por algún autómata de la clase.
Los autómatas no deterministas de Büchi, de paridad, de Rabin, de Streett y de Muller, respectivamente, reconocen todos exactamente la misma clase de ω-lenguajes. [1] Estos se conocen como el cierre ω-Kleene de los lenguajes regulares o como los ω-lenguajes regulares . Utilizando diferentes pruebas también se puede demostrar que los autómatas deterministas de paridad, de Rabin, de Streett y de Muller reconocen todos los ω-lenguajes regulares. De esto se deduce que la clase de ω-lenguajes regulares está cerrada bajo complementación. Sin embargo, el ejemplo anterior muestra que la clase de autómatas deterministas de Büchi es estrictamente más débil.
Como los autómatas no deterministas de Muller, Rabin, Streett, de paridad y de Büchi son igualmente expresivos, se pueden traducir entre sí. Utilicemos la siguiente abreviatura : por ejemplo, NB significa autómata no determinista de Büchi ω, mientras que DP significa autómata determinista de paridad ω. Entonces se cumple lo siguiente.
Se puede encontrar una descripción completa de las traducciones en la fuente web referenciada. [3]
Los ω-autómatas se pueden utilizar para demostrar la decidibilidad de S1S, la teoría monádica de segundo orden (MSO) de números naturales bajo sucesor. Los autómatas de árbol infinito extienden los ω-autómatas a árboles infinitos y se pueden utilizar para demostrar la decidibilidad de S2S , la teoría MSO con dos sucesores, y esto se puede extender a la teoría MSO de grafos con ancho de árbol acotado (dado un límite fijo) .