.jpeg/1280px-Newton's_rings_(650nm_red_laser_light).jpeg)
Los anillos de Newton son un fenómeno en el que se crea un patrón de interferencia por la reflexión de la luz entre dos superficies, normalmente una superficie esférica y una superficie plana adyacente que se toca. Recibe su nombre en honor a Isaac Newton , quien investigó el efecto en 1666. Cuando se observan con luz monocromática , los anillos de Newton aparecen como una serie de anillos concéntricos, brillantes y oscuros, alternados y centrados en el punto de contacto entre las dos superficies. Cuando se observan con luz blanca, forman un patrón de anillos concéntricos de colores del arco iris porque las diferentes longitudes de onda de la luz interfieren en diferentes espesores de la capa de aire entre las superficies.
El fenómeno fue descrito por primera vez por Robert Hooke en su libro Micrographia de 1665. Su nombre deriva del matemático y físico Sir Isaac Newton, quien estudió el fenómeno en 1666 mientras estaba recluido en su casa de Lincolnshire en la época de la Gran Plaga que había cerrado el Trinity College de Cambridge. Registró sus observaciones en un ensayo titulado "De los colores". El fenómeno se convirtió en una fuente de disputa entre Newton, que favorecía una naturaleza corpuscular de la luz, y Hooke, que favorecía una naturaleza ondulatoria de la luz. [1] Newton no publicó su análisis hasta después de la muerte de Hooke, como parte de su tratado " Opticks ", publicado en 1704.
El patrón se crea colocando un vidrio curvado ligeramente convexo sobre un vidrio plano óptico . Las dos piezas de vidrio hacen contacto solo en el centro. En otros puntos hay un pequeño espacio de aire entre las dos superficies, que aumenta con la distancia radial desde el centro, como se muestra en la figura 3.
Considere la luz monocromática (de un solo color) que incide desde arriba y que se refleja tanto en la superficie inferior de la lente superior como en la superficie superior del plano óptico debajo de ella. [2] La luz pasa a través de la lente de vidrio hasta que llega al límite vidrio-aire, donde la luz transmitida pasa de un valor de índice de refracción ( n ) más alto a un valor n más bajo . La luz transmitida pasa a través de este límite sin cambio de fase. La luz reflejada que experimenta reflexión interna (alrededor del 4% del total) tampoco tiene cambio de fase. La luz que se transmite al aire viaja una distancia, t , antes de reflejarse en la superficie plana de abajo. La reflexión en este límite aire-vidrio causa un cambio de fase de medio ciclo (180°) porque el aire tiene un índice de refracción más bajo que el vidrio. La luz reflejada en la superficie inferior regresa una distancia de (nuevamente) t y pasa nuevamente a la lente. La longitud de trayectoria adicional es igual al doble del espacio entre las superficies. Los dos rayos reflejados interferirán de acuerdo con el cambio de fase total causado por la longitud de trayectoria adicional 2 t y por el cambio de fase de medio ciclo inducido en la reflexión en la superficie plana. Cuando la distancia 2 t es cero (la lente toca la superficie plana óptica), las ondas interfieren destructivamente, por lo que la región central del patrón está oscura, como se muestra en la figura 2.
Un análisis similar para la iluminación del dispositivo desde abajo en lugar de desde arriba muestra que en este caso la parte central del patrón es brillante, no oscura, como se muestra en la figura 1. Cuando la luz no es monocromática, la posición radial del patrón de franjas tiene una apariencia de "arcoíris", como se muestra en la figura 5.
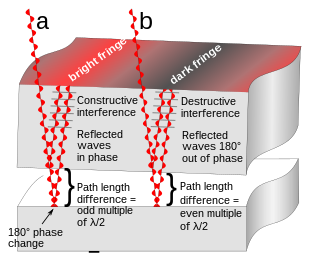
(Fig. 4a): En las zonas donde la diferencia de longitud de trayectoria entre los dos rayos es igual a un múltiplo impar de la mitad de la longitud de onda (λ/2) de las ondas de luz, las ondas reflejadas estarán en fase , por lo que los "valles" y "picos" de las ondas coinciden. Por lo tanto, las ondas se reforzarán (se sumarán) y la intensidad de la luz reflejada resultante será mayor. Como resultado, se observará allí una zona brillante.
(Fig. 4b): En otros lugares, donde la diferencia de longitud de trayectoria es igual a un múltiplo par de la mitad de la longitud de onda, las ondas reflejadas estarán desfasadas 180° , por lo que un "valle" de una onda coincide con un "pico" de la otra. Por lo tanto, las ondas se cancelarán (se restarán) y la intensidad de luz resultante será más débil o nula. Como resultado, se observará allí una zona oscura. Debido a la inversión de fase de 180° debida a la reflexión del rayo inferior, el centro donde se tocan las dos piezas está oscuro.
Esta interferencia da como resultado un patrón de líneas o bandas brillantes y oscuras llamadas " franjas de interferencia " que se observan en la superficie. Estas son similares a las líneas de contorno en los mapas, que revelan diferencias en el espesor del espacio de aire. El espacio entre las superficies es constante a lo largo de una franja. La diferencia de longitud de trayectoria entre dos franjas brillantes u oscuras adyacentes es una longitud de onda λ de la luz, por lo que la diferencia en el espacio entre las superficies es la mitad de la longitud de onda. Como la longitud de onda de la luz es tan pequeña, esta técnica puede medir desviaciones muy pequeñas de la planitud. Por ejemplo, la longitud de onda de la luz roja es de aproximadamente 700 nm, por lo que al usar luz roja la diferencia de altura entre dos franjas es la mitad, o 350 nm, aproximadamente 1 ⁄ 100 del diámetro de un cabello humano. Como el espacio entre los vidrios aumenta radialmente desde el centro, las franjas de interferencia forman anillos concéntricos. Para superficies de vidrio que no son axialmente simétricas, las franjas no serán anillos sino que tendrán otras formas.
Para la iluminación desde arriba, con un centro oscuro, el radio del anillo brillante N está dado por donde N es el número de anillo brillante, R es el radio de curvatura de la lente de vidrio a través de la cual pasa la luz y λ es la longitud de onda de la luz. La fórmula anterior también es aplicable para los anillos oscuros para el patrón de anillos obtenido por luz transmitida.
Dada la distancia radial de un anillo brillante, r , y un radio de curvatura de la lente, R , el espacio de aire entre las superficies de vidrio, t , se da con una buena aproximación mediante
donde se ignora el efecto de ver el patrón en un ángulo oblicuo a los rayos incidentes.
El fenómeno de los anillos de Newton se explica sobre la misma base que la interferencia de película delgada , incluidos efectos como los "arcoíris" que se ven en películas delgadas de aceite sobre el agua o en las pompas de jabón. La diferencia es que aquí la "película delgada" es una capa delgada de aire.
![{\displaystyle r_{N}=\left[\lambda R\left(N-{1 \sobre 2}\right)\right]^{1/2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42e6b239fd5a47ddcdddcb24d6371338e82e2fc8)
