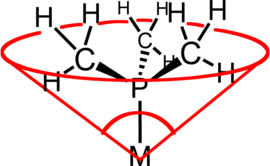
En química de coordinación , el ángulo de cono del ligando (θ) es una medida del volumen estérico de un ligando en un complejo de coordinación de un metal de transición . Se define como el ángulo sólido formado con el metal en el vértice de un cono y el borde más externo de las esferas de van der Waals de los átomos del ligando en el perímetro de la base del cono. Los ligandos de fosfina terciaria se clasifican comúnmente utilizando este parámetro, pero el método se puede aplicar a cualquier ligando. El término ángulo de cono fue introducido por primera vez por Chadwick A. Tolman , un químico investigador de DuPont . Tolman desarrolló originalmente el método para ligandos de fosfina en complejos de níquel, determinándolos a partir de mediciones de modelos físicos precisos. [1] [2] [3]
El concepto de ángulo de cono se visualiza más fácilmente con ligandos simétricos, p. ej. PR 3 . Pero el enfoque se ha refinado para incluir ligandos menos simétricos del tipo PRR′R″ así como difosfinas. En tales casos asimétricos, los semiángulos de los ángulos sustituyentes, θ yo/2 , se promedian y luego se duplican para encontrar el ángulo de cono total, θ . En el caso de las difosfinas, el θ yo/2 de la estructura principal se aproxima a la mitad del ángulo de mordida del quelato , asumiendo un ángulo de mordida de 74°, 85° y 90° para difosfinas con estructuras principales de metileno, etileno y propileno, respectivamente. El ángulo del cono de Manz suele ser más fácil de calcular que el ángulo del cono de Tolman: [4] [ aclaración necesaria ]
El método del ángulo cónico de Tolman asume datos de enlace empíricos y define el perímetro como la circunscripción máxima posible de un sustituyente idealizado de giro libre. La longitud del enlace metal-ligando en el modelo de Tolman se determinó empíricamente a partir de estructuras cristalinas de complejos tetraédricos de níquel. Por el contrario, el concepto de ángulo sólido deriva tanto la longitud del enlace como el perímetro a partir de estructuras cristalinas empíricas de estado sólido. [5] [6] Cada sistema tiene sus ventajas.
Si se conoce la geometría de un ligando, ya sea mediante cristalografía o cálculos, se puede calcular un ángulo de cono exacto ( θ ). [7] [8] [9] No se hacen suposiciones sobre la geometría, a diferencia del método de Tolman.
El concepto de ángulo de cono es de importancia práctica en la catálisis homogénea porque el tamaño del ligando afecta la reactividad del centro metálico unido. En un ejemplo, [10] la selectividad de los catalizadores de hidroformilación está fuertemente influenciada por el tamaño de los coligandos. A pesar de ser monovalentes , algunas fosfinas son lo suficientemente grandes como para ocupar más de la mitad de la esfera de coordinación de un centro metálico. Investigaciones recientes han descubierto que otros descriptores (como el porcentaje de volumen enterrado) son más precisos que el ángulo de cono para capturar los efectos estéricos relevantes del ligando o ligantes de fosfina cuando se unen al centro metálico. [11]