En física , el espacio-tiempo , también llamado continuo espacio-tiempo , es un modelo matemático que fusiona las tres dimensiones del espacio y la única dimensión del tiempo en un único continuo de cuatro dimensiones . Los diagramas de espacio-tiempo son útiles para visualizar y comprender los efectos relativistas , como la forma en que los diferentes observadores perciben dónde y cuándo ocurren los eventos.
Hasta principios del siglo XX, se suponía que la geometría tridimensional del universo (su descripción en términos de ubicaciones, formas, distancias y direcciones) era distinta del tiempo (la medición de cuándo ocurren los eventos dentro del universo). Sin embargo, el espacio y el tiempo adquirieron nuevos significados con la transformación de Lorentz y la teoría especial de la relatividad .
En 1908, Hermann Minkowski presentó una interpretación geométrica de la relatividad especial que fusionaba el tiempo y las tres dimensiones espaciales del espacio en un único continuo de cuatro dimensiones, conocido hoy como espacio de Minkowski . Esta interpretación resultó vital para la teoría general de la relatividad , según la cual el espacio-tiempo está curvado por la masa y la energía .
La mecánica clásica no relativista considera el tiempo como una cantidad universal de medida que es uniforme en todo su alcance, está separada del espacio y es aceptada por todos los observadores. La mecánica clásica supone que el tiempo tiene una velocidad constante de paso, independiente del estado de movimiento del observador o de cualquier elemento externo. [1] Supone que el espacio es euclidiano : supone que el espacio sigue la geometría del sentido común. [2]
En el contexto de la relatividad especial , el tiempo no puede separarse de las tres dimensiones del espacio, porque la velocidad observada a la que pasa el tiempo para un objeto depende de la velocidad del objeto en relación con el observador. [3] : 214–217 La relatividad general proporciona una explicación de cómo los campos gravitacionales pueden ralentizar el paso del tiempo de un objeto visto por un observador fuera del campo.
En el espacio ordinario, una posición se especifica mediante tres números, conocidos como dimensiones . En el sistema de coordenadas cartesianas , a menudo se denominan x , y y z . Un punto en el espacio-tiempo se denomina evento y requiere que se especifiquen cuatro números: la ubicación tridimensional en el espacio, más la posición en el tiempo (Fig. 1). Un evento se representa mediante un conjunto de coordenadas x , y , z y t . [4] El espacio-tiempo es, por tanto, cuatridimensional .
A diferencia de las analogías utilizadas en los escritos populares para explicar eventos, como los petardos o las chispas, los eventos matemáticos tienen duración cero y representan un único punto en el espacio-tiempo. [5] Aunque es posible estar en movimiento en relación con el estallido de un petardo o una chispa, no es posible que un observador esté en movimiento en relación con un evento.
La trayectoria de una partícula a través del espacio-tiempo puede considerarse una secuencia de eventos. La serie de eventos puede vincularse entre sí para formar una curva que representa el progreso de la partícula a través del espacio-tiempo. Esa trayectoria se denomina línea del universo de la partícula . [6] : 105
Matemáticamente, el espacio-tiempo es una variedad , es decir, parece localmente "plana" cerca de cada punto de la misma manera que, a escalas suficientemente pequeñas, la superficie de un globo parece ser plana. [7] Un factor de escala (convencionalmente llamado velocidad de la luz ) relaciona las distancias medidas en el espacio con las distancias medidas en el tiempo. La magnitud de este factor de escala (casi 300.000 kilómetros o 190.000 millas en el espacio son equivalentes a un segundo en el tiempo), junto con el hecho de que el espacio-tiempo es una variedad, implica que a velocidades ordinarias, no relativistas y a distancias ordinarias, a escala humana, hay poco que los humanos puedan observar que sea notablemente diferente de lo que podrían observar si el mundo fuera euclidiano. Fue recién con el advenimiento de mediciones científicas sensibles a mediados del siglo XIX, como el experimento de Fizeau y el experimento de Michelson-Morley , que comenzaron a notarse discrepancias desconcertantes entre las observaciones y las predicciones basadas en el supuesto implícito del espacio euclidiano. [8]

En la relatividad especial, un observador se refiere, en la mayoría de los casos, a un marco de referencia desde el cual se mide un conjunto de objetos o eventos. Este uso difiere significativamente del significado común del término en inglés. Los marcos de referencia son construcciones inherentemente no locales y, según este uso del término, no tiene sentido hablar de un observador como si tuviera una ubicación. [9]
En la figura 1-1, imaginemos que el marco en cuestión está equipado con una densa red de relojes, sincronizados dentro de este marco de referencia, que se extiende indefinidamente a lo largo de las tres dimensiones del espacio. Cualquier ubicación específica dentro de la red no es importante. La red de relojes se utiliza para determinar el tiempo y la posición de los eventos que tienen lugar dentro de todo el marco. El término observador se refiere a todo el conjunto de relojes asociados con un marco de referencia inercial. [9] : 17–22
En este caso idealizado, cada punto del espacio tiene un reloj asociado y, por lo tanto, los relojes registran cada evento instantáneamente, sin demora temporal entre un evento y su registro. Un observador real verá una demora entre la emisión de una señal y su detección debido a la velocidad de la luz. Para sincronizar los relojes, en la reducción de datos posterior a un experimento, se corregirá la hora en la que se recibe una señal para reflejar su hora real si hubiera sido registrada por una red idealizada de relojes. [9] : 17–22
En muchos libros sobre relatividad especial, especialmente en los más antiguos, la palabra "observador" se utiliza en el sentido más corriente de la palabra. El contexto suele dejar claro qué significado se ha adoptado.
Los físicos distinguen entre lo que se mide u observa , una vez descontados los retrasos en la propagación de la señal, y lo que se ve visualmente sin dichas correcciones. No entender la diferencia entre lo que se mide y lo que se ve es la fuente de mucha confusión entre los estudiantes de relatividad. [10]
A mediados del siglo XIX, varios experimentos, como la observación de la mancha de Arago y las mediciones diferenciales de la velocidad de la luz en el aire frente a la del agua, se consideraron que habían demostrado la naturaleza ondulatoria de la luz en oposición a una teoría corpuscular . [11] Entonces se asumió que la propagación de ondas requería la existencia de un medio ondulatorio ; en el caso de las ondas de luz, se consideró que este era un hipotético éter luminífero . [nota 1] Los diversos intentos de establecer las propiedades de este medio hipotético arrojaron resultados contradictorios. Por ejemplo, el experimento de Fizeau de 1851, realizado por el físico francés Hippolyte Fizeau , demostró que la velocidad de la luz en el agua en movimiento era menor que la suma de la velocidad de la luz en el aire más la velocidad del agua en una cantidad dependiente del índice de refracción del agua. [12]
Entre otras cuestiones, la dependencia del arrastre parcial del éter implicado por este experimento en el índice de refracción (que depende de la longitud de onda) llevó a la desagradable conclusión de que el éter fluye simultáneamente a diferentes velocidades para diferentes colores de luz. [13] El experimento de Michelson-Morley de 1887 (Fig. 1-2) no mostró ninguna influencia diferencial de los movimientos de la Tierra a través del éter hipotético en la velocidad de la luz, y la explicación más probable, el arrastre completo del éter, estaba en conflicto con la observación de la aberración estelar . [8]
George Francis FitzGerald en 1889, [14] y Hendrik Lorentz en 1892 propusieron de forma independiente que los cuerpos materiales que viajaban a través del éter fijo se veían afectados físicamente por su paso, contrayéndose en la dirección del movimiento en una cantidad que era exactamente la necesaria para explicar los resultados negativos del experimento de Michelson-Morley. No se producen cambios de longitud en direcciones transversales a la dirección del movimiento.
En 1904, Lorentz había ampliado su teoría de tal manera que había llegado a ecuaciones formalmente idénticas a las que Einstein derivaría más tarde, es decir, la transformación de Lorentz . [15] Como teoría de la dinámica (el estudio de las fuerzas y los pares y su efecto sobre el movimiento), su teoría suponía deformaciones físicas reales de los componentes físicos de la materia. [16] : 163–174 Las ecuaciones de Lorentz predijeron una cantidad que llamó tiempo local , con la que podía explicar la aberración de la luz , el experimento de Fizeau y otros fenómenos.
Henri Poincaré fue el primero en combinar el espacio y el tiempo en el espacio-tiempo. [17] [18] : 73–80, 93–95 Argumentó en 1898 que la simultaneidad de dos eventos es una cuestión de convención. [19] [nota 2] En 1900, reconoció que el "tiempo local" de Lorentz es en realidad lo que indican los relojes en movimiento aplicando una definición explícitamente operacional de sincronización de relojes asumiendo una velocidad de la luz constante. [nota 3] En 1900 y 1904, sugirió la indetectabilidad inherente del éter enfatizando la validez de lo que llamó el principio de relatividad . En 1905/1906 [20] perfeccionó matemáticamente la teoría de los electrones de Lorentz para ponerla de acuerdo con el postulado de la relatividad.
Mientras discutía varias hipótesis sobre la gravitación invariante de Lorentz, introdujo el concepto innovador de un espacio-tiempo de cuatro dimensiones al definir varios vectores de cuatro dimensiones , a saber, cuatro posiciones , cuatro velocidades y cuatro fuerzas . [21] [22] Sin embargo, no persiguió el formalismo de cuatro dimensiones en artículos posteriores, afirmando que esta línea de investigación parecía "implicar un gran dolor para un beneficio limitado", concluyendo finalmente "que el lenguaje tridimensional parece el más adecuado para la descripción de nuestro mundo". [22] Incluso en 1909, Poincaré continuó describiendo la interpretación dinámica de la transformada de Lorentz. [16] : 163–174
En 1905, Albert Einstein analizó la relatividad especial en términos de cinemática (el estudio de los cuerpos en movimiento sin referencia a fuerzas) en lugar de dinámica. Sus resultados eran matemáticamente equivalentes a los de Lorentz y Poincaré. Los obtuvo al reconocer que toda la teoría puede construirse sobre dos postulados: el principio de relatividad y el principio de la constancia de la velocidad de la luz. Su trabajo estaba lleno de vívidas imágenes que involucraban el intercambio de señales de luz entre relojes en movimiento, mediciones cuidadosas de las longitudes de varillas en movimiento y otros ejemplos similares. [23] [nota 4]
En 1905, Einstein superó los intentos previos de una relación electromagnética masa -energía al introducir la equivalencia general de masa y energía , que fue fundamental para su posterior formulación del principio de equivalencia en 1907, que declara la equivalencia de la masa inercial y gravitacional. Al utilizar la equivalencia masa-energía, Einstein demostró que la masa gravitacional de un cuerpo es proporcional a su contenido de energía, lo que fue uno de los primeros resultados en el desarrollo de la relatividad general . Si bien parecería que al principio no pensó geométricamente sobre el espacio-tiempo, [3] : 219 en el desarrollo posterior de la relatividad general, Einstein incorporó plenamente el formalismo del espacio-tiempo.
Cuando Einstein publicó en 1905, otro de sus competidores, su antiguo profesor de matemáticas Hermann Minkowski , también había llegado a la mayoría de los elementos básicos de la relatividad especial. Max Born relató una reunión que había concertado con Minkowski, con la intención de ser su alumno/colaborador: [25]
Fui a Colonia, conocí a Minkowski y escuché su célebre conferencia «Espacio y tiempo», pronunciada el 2 de septiembre de 1908. [...] Más tarde me dijo que le causó un gran impacto cuando Einstein publicó su artículo en el que se afirmaba la equivalencia de los diferentes tiempos locales de los observadores que se movían unos con respecto a otros; pues había llegado a las mismas conclusiones de forma independiente, pero no las publicó porque deseaba primero elaborar la estructura matemática en todo su esplendor. Nunca reivindicó la prioridad y siempre concedió a Einstein su parte plena en el gran descubrimiento.
Minkowski se había interesado por el estado de la electrodinámica después de los experimentos disruptivos de Michelson al menos desde el verano de 1905, cuando Minkowski y David Hilbert dirigieron un seminario avanzado al que asistieron físicos notables de la época para estudiar los artículos de Lorentz, Poincaré y otros. Minkowski vio el trabajo de Einstein como una extensión del de Lorentz, y fue influenciado más directamente por Poincaré. [26]

El 5 de noviembre de 1907 (poco más de un año antes de su muerte), Minkowski presentó su interpretación geométrica del espacio-tiempo en una conferencia ante la Sociedad Matemática de Göttingen con el título El principio de relatividad ( Das Relativitätsprinzip ). [nota 5] El 21 de septiembre de 1908, Minkowski presentó su charla Espacio y tiempo ( Raum und Zeit ), [27] ante la Sociedad Alemana de Científicos y Médicos. Las palabras iniciales de Espacio y tiempo incluyen la declaración de Minkowski de que "de ahora en adelante, el espacio para sí mismo y el tiempo para sí mismo se reducirán completamente a una mera sombra, y solo algún tipo de unión de los dos preservará la independencia". Espacio y tiempo incluyó la primera presentación pública de diagramas de espacio-tiempo (Fig. 1-4), e incluyó una notable demostración de que el concepto de intervalo invariante (discutido más adelante), junto con la observación empírica de que la velocidad de la luz es finita, permite la derivación de la totalidad de la relatividad especial. [nota 6]
El concepto de espacio-tiempo y el grupo de Lorentz están estrechamente relacionados con ciertos tipos de geometrías esféricas , hiperbólicas o conformes y sus grupos de transformación ya desarrollados en el siglo XIX, en los que se utilizan intervalos invariantes análogos al intervalo espacio-tiempo . [nota 7]
Einstein, por su parte, inicialmente desestimó la interpretación geométrica de Minkowski de la relatividad especial, considerándola überflüssige Gelehrsamkeit (erudición superflua). Sin embargo, para completar su búsqueda de la relatividad general que comenzó en 1907, la interpretación geométrica de la relatividad resultó vital. En 1916, Einstein reconoció plenamente su deuda con Minkowski, cuya interpretación facilitó enormemente la transición a la relatividad general. [16] : 151–152 Dado que existen otros tipos de espacio-tiempo, como el espacio-tiempo curvo de la relatividad general, el espacio-tiempo de la relatividad especial se conoce hoy como espacio-tiempo de Minkowski.
En tres dimensiones, la distancia entre dos puntos se puede definir utilizando el teorema de Pitágoras :
Aunque dos observadores pueden medir la posición x , y y z de los dos puntos utilizando diferentes sistemas de coordenadas, la distancia entre los puntos será la misma para ambos, suponiendo que estén midiendo utilizando las mismas unidades. La distancia es "invariante".
Sin embargo, en la relatividad especial, la distancia entre dos puntos ya no es la misma si la miden dos observadores diferentes, cuando uno de ellos se mueve, debido a la contracción de Lorentz . La situación es aún más complicada si los dos puntos están separados tanto en el tiempo como en el espacio. Por ejemplo, si un observador ve que dos eventos ocurren en el mismo lugar, pero en diferentes momentos, una persona que se mueve con respecto al primer observador verá que los dos eventos ocurren en lugares diferentes, porque el punto de vista en movimiento se ve a sí mismo como estacionario, y la posición del evento como alejándose o acercándose. Por lo tanto, se debe utilizar una medida diferente para medir la "distancia" efectiva entre dos eventos. [31] : 48–50, 100–102
En el espacio-tiempo de cuatro dimensiones, el análogo de la distancia es el intervalo. Aunque el tiempo entra como una cuarta dimensión, se trata de manera diferente a las dimensiones espaciales. Por lo tanto, el espacio de Minkowski difiere en aspectos importantes del espacio euclidiano de cuatro dimensiones . La razón fundamental para fusionar el espacio y el tiempo en el espacio-tiempo es que el espacio y el tiempo no son invariantes por separado, lo que quiere decir que, en las condiciones adecuadas, diferentes observadores no estarán de acuerdo sobre la duración del tiempo entre dos eventos (debido a la dilatación del tiempo ) o la distancia entre los dos eventos (debido a la contracción de la longitud ). La relatividad especial proporciona un nuevo invariante, llamado intervalo espacio-temporal , que combina distancias en el espacio y en el tiempo. Todos los observadores que midan el tiempo y la distancia entre dos eventos cualesquiera terminarán calculando el mismo intervalo espacio-temporal. Supongamos que un observador mide dos eventos separados en el tiempo por y una distancia espacial . Entonces, el intervalo espacio-temporal al cuadrado entre los dos eventos que están separados por una distancia en el espacio y por en la coordenada es: [32]
o para tres dimensiones espaciales,
La constante de la velocidad de la luz convierte las unidades de tiempo (como los segundos) en unidades de espacio (como los metros). El intervalo al cuadrado es una medida de separación entre los eventos A y B que están separados en el tiempo y además separados en el espacio, ya sea porque hay dos objetos separados que experimentan eventos o porque un solo objeto en el espacio se mueve inercialmente entre sus eventos. El intervalo de separación es la diferencia entre el cuadrado de la distancia espacial que separa el evento B del evento A y el cuadrado de la distancia espacial recorrida por una señal de luz en ese mismo intervalo de tiempo . Si la separación de eventos se debe a una señal de luz, entonces esta diferencia se desvanece y .
Cuando los eventos considerados son infinitesimalmente cercanos entre sí, entonces podemos escribir
En un marco inercial diferente, digamos con coordenadas , el intervalo espacio-temporal se puede escribir en la misma forma que arriba. Debido a la constancia de la velocidad de la luz, los eventos de luz en todos los marcos inerciales pertenecen al intervalo cero, . Para cualquier otro evento infinitesimal donde , se puede probar que lo que a su vez al integrar conduce a . [33] : 2 La invariancia del intervalo espacio-temporal entre los mismos eventos para todos los marcos de referencia inerciales es uno de los resultados fundamentales de la teoría especial de la relatividad.
Aunque por brevedad, con frecuencia se ven expresiones de intervalo expresadas sin deltas, incluso en la mayor parte de la discusión siguiente, debe entenderse que, en general, significa , etc. Siempre nos preocupan las diferencias de los valores de coordenadas espaciales o temporales que pertenecen a dos eventos y, dado que no hay un origen preferido, los valores de coordenadas individuales no tienen un significado esencial.

La ecuación anterior es similar al teorema de Pitágoras, excepto que hay un signo menos entre los términos y . El intervalo del espacio-tiempo es la cantidad, no en sí misma. La razón es que, a diferencia de las distancias en la geometría euclidiana, los intervalos en el espacio-tiempo de Minkowski pueden ser negativos. En lugar de tratar con raíces cuadradas de números negativos, los físicos suelen considerarlo como un símbolo distinto en sí mismo, en lugar del cuadrado de algo. [3] : 217
En general, puede asumir cualquier valor de número real. Si es positivo, el intervalo de espacio-tiempo se denomina similar al tiempo . Dado que la distancia espacial recorrida por cualquier objeto masivo es siempre menor que la distancia recorrida por la luz durante el mismo intervalo de tiempo, los intervalos positivos son siempre similares al tiempo. Si es negativo, se dice que el intervalo de espacio-tiempo es similar al espacio . Los intervalos de espacio-tiempo son iguales a cero cuando En otras palabras, el intervalo de espacio-tiempo entre dos eventos en la línea del universo de algo que se mueve a la velocidad de la luz es cero. Tal intervalo se denomina similar a la luz o nulo . Un fotón que llega a nuestro ojo desde una estrella distante no habrá envejecido, a pesar de haber pasado (desde nuestra perspectiva) años en su paso. [31] : 48–50
Un diagrama de espacio-tiempo se dibuja típicamente con un solo espacio y una sola coordenada de tiempo. La Fig. 2-1 presenta un diagrama de espacio-tiempo que ilustra las líneas del mundo (es decir, las trayectorias en el espacio-tiempo) de dos fotones, A y B, que se originan del mismo evento y van en direcciones opuestas. Además, C ilustra la línea del mundo de un objeto más lento que la velocidad de la luz. La coordenada de tiempo vertical está escalada de modo que tenga las mismas unidades (metros) que la coordenada espacial horizontal. Dado que los fotones viajan a la velocidad de la luz, sus líneas del mundo tienen una pendiente de ±1. [31] : 23–25 En otras palabras, cada metro que un fotón viaja hacia la izquierda o la derecha requiere aproximadamente 3,3 nanosegundos de tiempo.


Para comprender mejor cómo se comparan entre sí las coordenadas del espacio-tiempo medidas por observadores en diferentes marcos de referencia , es útil trabajar con una configuración simplificada con marcos en una configuración estándar. Con cuidado, esto permite simplificar las matemáticas sin perder generalidad en las conclusiones a las que se llega. En la figura 2-2, se muestran dos marcos de referencia galileanos (es decir, marcos convencionales de 3 espacios) en movimiento relativo. El marco S pertenece a un primer observador O, y el marco S′ (pronunciado "S prima") pertenece a un segundo observador O′.
La figura 2-3a vuelve a dibujar la figura 2-2 con una orientación diferente. La figura 2-3b ilustra un diagrama de espacio-tiempo relativista desde el punto de vista del observador O. Puesto que S y S′ están en configuración estándar, sus orígenes coinciden en los tiempos t = 0 en el sistema de referencia S y t ′ = 0 en el sistema de referencia S′. El eje ct ′ pasa por los eventos en el sistema de referencia S′ que tienen x ′ = 0. Pero los puntos con x ′ = 0 se mueven en la dirección x del sistema de referencia S con velocidad v , de modo que no coinciden con el eje ct en ningún tiempo distinto de cero. Por lo tanto, el eje ct ′ está inclinado con respecto al eje ct en un ángulo θ dado por [31] : 23–31
El eje x ′ también está inclinado con respecto al eje x . Para determinar el ángulo de esta inclinación, recordamos que la pendiente de la línea del universo de un pulso de luz es siempre ±1. La figura 2-3c presenta un diagrama de espacio-tiempo desde el punto de vista del observador O′. El evento P representa la emisión de un pulso de luz en x ′ = 0, ct ′ = − a . El pulso se refleja desde un espejo situado a una distancia a de la fuente de luz (evento Q), y regresa a la fuente de luz en x ′ = 0, ct ′ = a (evento R).
Los mismos eventos P, Q, R se representan en la Fig. 2-3b en el marco del observador O. Las trayectorias de la luz tienen pendientes = 1 y −1, de modo que △PQR forma un triángulo rectángulo con PQ y QR ambos a 45 grados respecto de los ejes x y ct . Como OP = OQ = OR, el ángulo entre x ′ y x también debe ser θ . [6] : 113–118
Mientras que el marco en reposo tiene ejes de espacio y tiempo que se encuentran en ángulos rectos, el marco en movimiento está dibujado con ejes que se encuentran en un ángulo agudo. Los marcos son en realidad equivalentes. [31] : 23–31 La asimetría se debe a distorsiones inevitables en cómo las coordenadas del espacio-tiempo pueden mapearse en un plano cartesiano , y no debe considerarse más extraña que la manera en que, en una proyección Mercator de la Tierra, los tamaños relativos de las masas de tierra cerca de los polos (Groenlandia y la Antártida) son altamente exagerados en relación con las masas de tierra cerca del Ecuador.

En la figura 2-4, el evento O está en el origen de un diagrama de espacio-tiempo, y las dos líneas diagonales representan todos los eventos que tienen un intervalo de espacio-tiempo cero con respecto al evento de origen. Estas dos líneas forman lo que se llama el cono de luz del evento O, ya que al agregar una segunda dimensión espacial (figura 2-5) se crea la apariencia de dos conos circulares rectos que se encuentran con sus vértices en O. Un cono se extiende hacia el futuro (t>0), el otro hacia el pasado (t<0).

Un cono de luz (doble) divide el espacio-tiempo en regiones separadas con respecto a su vértice. El interior del cono de luz futuro consta de todos los eventos que están separados del vértice por más tiempo (distancia temporal) del necesario para cruzar su distancia espacial a la velocidad de la luz; estos eventos comprenden el futuro temporal del evento O. Del mismo modo, el pasado temporal comprende los eventos interiores del cono de luz pasado. Por lo tanto, en intervalos temporales Δ ct es mayor que Δ x , lo que hace que los intervalos temporales sean positivos. [3] : 220
La región exterior al cono de luz consiste en eventos que están separados del evento O por más espacio del que se puede cruzar a la velocidad de la luz en el tiempo dado . Estos eventos comprenden la llamada región espacial del evento O, denotada como "En otro lugar" en la Fig. 2-4. Se dice que los eventos en el propio cono de luz son similares a la luz (o separados nulamente ) de O. Debido a la invariancia del intervalo espacio-temporal, todos los observadores asignarán el mismo cono de luz a cualquier evento dado y, por lo tanto, estarán de acuerdo con esta división del espacio-tiempo. [3] : 220
El cono de luz tiene un papel esencial dentro del concepto de causalidad . Es posible que una señal que no viaja más rápido que la velocidad de la luz viaje desde la posición y el tiempo de O a la posición y el tiempo de D (Fig. 2-4). Por lo tanto, es posible que el evento O tenga una influencia causal en el evento D. El cono de luz futuro contiene todos los eventos que podrían ser influenciados causalmente por O. Del mismo modo, es posible que una señal que no viaja más rápido que la velocidad de la luz viaje desde la posición y el tiempo de A, a la posición y el tiempo de O. El cono de luz pasado contiene todos los eventos que podrían tener una influencia causal en O. En contraste, suponiendo que las señales no pueden viajar más rápido que la velocidad de la luz, cualquier evento, como por ejemplo B o C, en la región espacial (Elsewhere), no puede afectar al evento O, ni puede ser afectado por el evento O que emplee dicha señalización. Bajo este supuesto, se excluye cualquier relación causal entre el evento O y cualquier evento en la región espacial de un cono de luz. [35]

Todos los observadores estarán de acuerdo en que, para cualquier evento dado, un evento dentro del cono de luz futuro del evento dado ocurre después del evento dado. De la misma manera, para cualquier evento dado, un evento dentro del cono de luz pasado del evento dado ocurre antes del evento dado. La relación antes-después observada para eventos separados en el tiempo permanece invariable sin importar cuál sea el marco de referencia del observador, es decir, sin importar cómo se esté moviendo el observador. La situación es bastante diferente para eventos separados en el espacio. La figura 2-4 se dibujó a partir del marco de referencia de un observador que se mueve en v = 0. A partir de este marco de referencia, se observa que el evento C ocurre después del evento O, y se observa que el evento B ocurre antes del evento O. [36]
Desde un marco de referencia diferente, el orden de estos eventos no relacionados causalmente puede invertirse. En particular, se observa que si dos eventos son simultáneos en un marco de referencia particular, están necesariamente separados por un intervalo espacial y, por lo tanto, están relacionados de manera no causal. La observación de que la simultaneidad no es absoluta, sino que depende del marco de referencia del observador, se denomina relatividad de la simultaneidad . [36]
La figura 2-6 ilustra el uso de diagramas de espacio-tiempo en el análisis de la relatividad de la simultaneidad. Los eventos en el espacio-tiempo son invariantes, pero los marcos de coordenadas se transforman como se discutió anteriormente para la figura 2-3. Los tres eventos (A, B, C) son simultáneos desde el marco de referencia de un observador que se mueve en v = 0. Desde el marco de referencia de un observador que se mueve en v = 0.3 c , los eventos parecen ocurrir en el orden C, B, A. Desde el marco de referencia de un observador que se mueve en v = −0.5 c , los eventos parecen ocurrir en el orden A, B, C . La línea blanca representa un plano de simultaneidad que se mueve desde el pasado del observador al futuro del observador, resaltando los eventos que residen en él. El área gris es el cono de luz del observador, que permanece invariante.
Un intervalo de espacio-tiempo similar al espacio da la misma distancia que un observador mediría si los eventos que se están midiendo fueran simultáneos para el observador. Un intervalo de espacio-tiempo similar al espacio proporciona, por lo tanto, una medida de la distancia propia , es decir, la distancia verdadera = Del mismo modo, un intervalo de espacio-tiempo similar al tiempo da la misma medida del tiempo que se presentaría por el tictac acumulativo de un reloj que se mueve a lo largo de una línea de universo dada. Un intervalo de espacio-tiempo similar al tiempo proporciona, por lo tanto, una medida del tiempo propio = [3] : 220–221

En el espacio euclidiano (que tiene solo dimensiones espaciales), el conjunto de puntos equidistantes (usando la métrica euclidiana) de algún punto forman un círculo (en dos dimensiones) o una esfera (en tres dimensiones). En el espacio-tiempo de Minkowski (1+1)-dimensional (que tiene una dimensión temporal y una espacial), los puntos a un intervalo de espacio-tiempo constante alejados del origen (usando la métrica de Minkowski) forman curvas dadas por las dos ecuaciones
con alguna constante real positiva. Estas ecuaciones describen dos familias de hipérbolas en un diagrama de espacio-tiempo x – ct , que se denominan hipérbolas invariantes .
En la figura 2-7a, cada hipérbola magenta conecta todos los eventos que tienen una separación espacial fija desde el origen, mientras que las hipérbolas verdes conectan eventos con una separación temporal igual.
Las hipérbolas magenta, que cruzan el eje x , son curvas temporales, es decir, representan trayectorias reales que pueden recorrer partículas (constantemente aceleradas) en el espacio-tiempo: Entre dos eventos cualesquiera en una hipérbola es posible una relación de causalidad, porque la inversa de la pendiente (que representa la velocidad necesaria) para todas las secantes es menor que . Por otro lado, las hipérbolas verdes, que cruzan el eje ct , son curvas espaciales porque todos los intervalos a lo largo de estas hipérbolas son intervalos espaciales: No es posible ninguna causalidad entre dos puntos cualesquiera en una de estas hipérbolas, porque todas las secantes representan velocidades mayores que .
La figura 2-7b refleja la situación en el espacio-tiempo de Minkowski (1+2)-dimensional (una temporal y dos espaciales) con los hiperboloides correspondientes. Las hipérbolas invariantes desplazadas por intervalos espaciales desde el origen generan hiperboloides de una hoja, mientras que las hipérbolas invariantes desplazadas por intervalos temporales desde el origen generan hiperboloides de dos hojas.
El límite (1+2)-dimensional entre hiperboloides espaciales y temporales, establecido por los eventos que forman un intervalo de espacio-tiempo cero hasta el origen, se forma degenerando los hiperboloides hasta el cono de luz. En (1+1)-dimensionales las hipérbolas degeneran hasta las dos líneas grises de 45° representadas en la Fig. 2-7a.
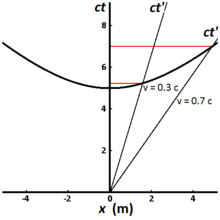
La figura 2-8 ilustra la hipérbola invariante para todos los eventos a los que se puede llegar desde el origen en un tiempo propio de 5 metros (aproximadamente1,67 × 10 −8 s ). Diferentes líneas del universo representan relojes que se mueven a diferentes velocidades. Un reloj que está estacionario con respecto al observador tiene una línea del universo que es vertical, y el tiempo transcurrido medido por el observador es el mismo que el tiempo propio. Para un reloj que se mueve a 0,3 c , el tiempo transcurrido medido por el observador es de 5,24 metros (1,75 × 10 −8 s ), mientras que para un reloj que viaja a 0,7 c , el tiempo transcurrido medido por el observador es de 7,00 metros (2,34 × 10 −8 s ). [3] : 220–221
Esto ilustra el fenómeno conocido como dilatación del tiempo . Los relojes que viajan más rápido tardan más (en el marco del observador) en marcar la misma cantidad de tiempo propio, y viajan más lejos a lo largo del eje x dentro de ese tiempo propio de lo que lo hubieran hecho sin la dilatación del tiempo. [3] : 220–221 La medición de la dilatación del tiempo por dos observadores en diferentes marcos de referencia inerciales es mutua. Si el observador O mide los relojes del observador O′ como si fueran más lentos en su marco, el observador O′ a su vez medirá los relojes del observador O como si fueran más lentos.

La contracción de la longitud , al igual que la dilatación del tiempo, es una manifestación de la relatividad de la simultaneidad. La medición de la longitud requiere la medición del intervalo espacio-temporal entre dos eventos que son simultáneos en nuestro marco de referencia. Pero los eventos que son simultáneos en un marco de referencia, en general, no lo son en otros marcos de referencia.
La figura 2-9 ilustra los movimientos de una varilla de 1 m que se desplaza a 0,5 c a lo largo del eje x . Los bordes de la banda azul representan las líneas de universo de los dos puntos finales de la varilla. La hipérbola invariante ilustra eventos separados del origen por un intervalo espacial de 1 m. Los puntos finales O y B medidos cuando t ′ = 0 son eventos simultáneos en el marco S′. Pero para un observador en el marco S, los eventos O y B no son simultáneos. Para medir la longitud, el observador en el marco S mide los puntos finales de la varilla tal como se proyectan sobre el eje x a lo largo de sus líneas de universo. La proyección de la lámina de universo de la varilla sobre el eje x produce la longitud escorzada OC. [6] : 125
(no ilustrado) Trazar una línea vertical a través de A de modo que intersecte el eje x ′ demuestra que, así como OB está acortado desde el punto de vista del observador O, OA también está acortado desde el punto de vista del observador O′. De la misma manera que cada observador mide los relojes del otro como si estuvieran atrasados, cada observador mide las reglas del otro como si estuvieran contraídas.
Con respecto a la contracción mutua de longitud, la figura 2-9 ilustra que los marcos primados y no primados se rotan mutuamente en un ángulo hiperbólico (análogo a los ángulos ordinarios en la geometría euclidiana). [nota 8] Debido a esta rotación, la proyección de una regla métrica primada sobre el eje x no primado se acorta, mientras que la proyección de una regla métrica no primada sobre el eje x′ primado también se acorta.
La dilatación mutua del tiempo y la contracción de la longitud tienden a parecer a los principiantes conceptos inherentemente contradictorios. Si un observador en el marco S mide un reloj, en reposo en el marco S', como si funcionara más lento que el suyo, mientras que S' se mueve a una velocidad v en S, entonces el principio de relatividad requiere que un observador en el marco S' mida de la misma manera un reloj en el marco S, que se mueve a una velocidad − v en S', como si funcionara más lento que el suyo. Cómo pueden funcionar dos relojes más lentos que el otro es una pregunta importante que "va al corazón de la comprensión de la relatividad especial". [3] : 198
Esta aparente contradicción se debe a que no se han tenido en cuenta correctamente las diferentes configuraciones de las mediciones necesarias relacionadas. Estas configuraciones permiten una explicación coherente de la única contradicción aparente . No se trata del tictac abstracto de dos relojes idénticos, sino de cómo medir en un marco la distancia temporal de dos tictacs de un reloj en movimiento. Resulta que para observar mutuamente la duración entre tictacs de relojes, cada uno en movimiento en el marco respectivo, deben intervenir diferentes conjuntos de relojes. Para medir en el marco S la duración del tictac de un reloj en movimiento W′ (en reposo en S′), se utilizan dos relojes adicionales sincronizados W 1 y W 2 en reposo en dos puntos arbitrariamente fijos en S con la distancia espacial d .
Por el contrario, para juzgar en el marco S′ la distancia temporal de dos eventos en un reloj en movimiento W (en reposo en S), se necesitan dos relojes en reposo en S′.
Los registros necesarios para los dos juicios, con "un reloj en movimiento" y "dos relojes en reposo" en S o S′ respectivamente, implican dos conjuntos diferentes, cada uno con tres relojes. Dado que hay diferentes conjuntos de relojes involucrados en las mediciones, no hay una necesidad inherente de que las mediciones sean recíprocamente "consistentes" de modo que, si un observador mide el reloj en movimiento como lento, el otro observador mide el reloj del primero como rápido. [3] : 198–199
La figura 2-10 ilustra la discusión previa de la dilatación mutua del tiempo con diagramas de Minkowski. La imagen superior refleja las mediciones como se ven desde el marco S "en reposo" con ejes rectangulares sin primar, y el marco S′ "moviéndose con v > 0", coordinado por ejes oblicuos con primar, inclinados hacia la derecha; la imagen inferior muestra el marco S′ "en reposo" con coordenadas rectangulares con primar, y el marco S "moviéndose con − v < 0", con ejes oblicuos sin primar, inclinados hacia la izquierda.
Cada línea trazada paralela a un eje espacial ( x , x ′ ) representa una línea de simultaneidad. Todos los eventos en dicha línea tienen el mismo valor temporal ( ct , ct ′ ). Del mismo modo, cada línea trazada paralela a un eje temporal ( ct , ct′ ) representa una línea de valores de coordenadas espaciales iguales ( x , x ′ ).
Para mostrar la dilatación mutua del tiempo inmediatamente en la imagen superior, el evento D puede construirse como el evento en x ′ = 0 (la ubicación del reloj W′ en S′), que es simultáneo a C ( OC tiene el mismo intervalo de espacio-tiempo que OA ) en S′. Esto muestra que el intervalo de tiempo OD es más largo que OA , lo que demuestra que el reloj "en movimiento" corre más lento. [6] : 124
En la imagen inferior, el sistema S se mueve con velocidad − v en el sistema S′ en reposo. La línea de mundo del reloj W es el eje ct (inclinado hacia la izquierda), la línea de mundo de W′ 1 es el eje vertical ct ′ y la línea de mundo de W′ 2 es la vertical que pasa por el evento C , con la coordenada ct ′ D. La hipérbola invariante que pasa por el evento C escala el intervalo de tiempo OC a OA , que es más corto que OD ; además, B se construye (similar a D en las imágenes superiores) como simultáneo a A en S, en x = 0. El resultado OB > OC corresponde nuevamente al anterior.
La palabra "medida" es importante. En física clásica, un observador no puede afectar a un objeto observado, pero el estado de movimiento del objeto puede afectar las observaciones que el observador hace del objeto.
Muchas introducciones a la relatividad especial ilustran las diferencias entre la relatividad galileana y la relatividad especial planteando una serie de "paradojas". Estas paradojas son, de hecho, problemas mal planteados, resultado de nuestra falta de familiaridad con velocidades comparables a la velocidad de la luz. La solución es resolver muchos problemas de la relatividad especial y familiarizarse con sus llamadas predicciones contraintuitivas. El enfoque geométrico para estudiar el espacio-tiempo se considera uno de los mejores métodos para desarrollar una intuición moderna. [37]
La paradoja de los gemelos es un experimento mental que involucra a gemelos idénticos, uno de los cuales hace un viaje al espacio en un cohete de alta velocidad, regresa a casa y descubre que el gemelo que permaneció en la Tierra ha envejecido más. Este resultado parece desconcertante porque cada gemelo observa al otro gemelo moverse, y por lo tanto, a primera vista, parecería que cada uno debería encontrar que el otro ha envejecido menos. La paradoja de los gemelos elude la justificación de la dilatación mutua del tiempo presentada anteriormente al evitar el requisito de un tercer reloj. [3] : 207 Sin embargo, la paradoja de los gemelos no es una verdadera paradoja porque se entiende fácilmente dentro del contexto de la relatividad especial.
La impresión de que existe una paradoja surge de una mala interpretación de lo que afirma la relatividad especial. La relatividad especial no declara que todos los marcos de referencia sean equivalentes, sino sólo los marcos inerciales. El marco de la gemela viajera no es inercial durante los períodos en que está acelerando. Además, la diferencia entre las gemelas es detectable observacionalmente: la gemela viajera necesita encender sus cohetes para poder regresar a casa, mientras que la gemela que se queda en casa no. [38] [nota 9]
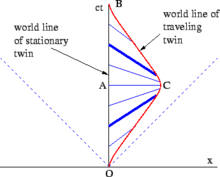
Estas distinciones deberían dar como resultado una diferencia en las edades de los gemelos. El diagrama de espacio-tiempo de la figura 2-11 presenta el caso simple de un gemelo que sale en línea recta a lo largo del eje x y regresa inmediatamente. Desde el punto de vista del gemelo que se queda en casa, no hay nada desconcertante en la paradoja de los gemelos en absoluto. El tiempo propio medido a lo largo de la línea del mundo del gemelo viajero de O a C, más el tiempo propio medido de C a B, es menor que el tiempo propio del gemelo que se queda en casa medido de O a A a B. Las trayectorias más complejas requieren integrar el tiempo propio entre los respectivos eventos a lo largo de la curva (es decir, la integral de trayectoria ) para calcular la cantidad total de tiempo propio experimentado por el gemelo viajero. [38]
Surgen complicaciones si se analiza la paradoja de los gemelos desde el punto de vista del gemelo viajero.
De ahora en adelante se utilizará la nomenclatura de Weiss, que designa al gemelo que se queda en casa como Terence y a la gemela que viaja como Stella. [38]
Stella no está en un marco inercial. Dado este hecho, a veces se afirma incorrectamente que la resolución completa de la paradoja de los gemelos requiere la relatividad general: [38]
Un análisis SR puro sería el siguiente: Analizado en el marco de reposo de Stella, ella está inmóvil durante todo el viaje. Cuando dispara sus cohetes para el cambio de dirección, experimenta una pseudofuerza que se asemeja a una fuerza gravitacional. [38] Las figuras 2-6 y 2-11 ilustran el concepto de líneas (planos) de simultaneidad: las líneas paralelas al eje x del observador (plano xy ) representan conjuntos de eventos que son simultáneos en el marco del observador. En la figura 2-11, las líneas azules conectan eventos en la línea del mundo de Terence que, desde el punto de vista de Stella , son simultáneos con eventos en su línea del mundo. (Terence, a su vez, observaría un conjunto de líneas horizontales de simultaneidad). A lo largo de los tramos de ida y vuelta del viaje de Stella, ella mide los relojes de Terence como si fueran más lentos que el suyo. Pero durante el giro (es decir, entre las líneas azules en negrita de la figura), se produce un cambio en el ángulo de sus líneas de simultaneidad, que corresponde a un rápido salto de los acontecimientos en la línea del mundo de Terence que Stella considera simultáneos con el suyo. Por lo tanto, al final de su viaje, Stella descubre que Terence ha envejecido más que ella. [38]
Aunque no se requiere la relatividad general para analizar la paradoja de los gemelos, la aplicación del principio de equivalencia de la relatividad general sí proporciona una visión adicional del tema. Stella no está estacionaria en un marco inercial. Analizada en el marco de reposo de Stella, está inmóvil durante todo el viaje. Cuando se desplaza por inercia, su marco de reposo es inercial, y el reloj de Terence parecerá ir más lento. Pero cuando dispara sus cohetes para dar la vuelta, su marco de reposo es un marco acelerado y experimenta una fuerza que la empuja como si estuviera en un campo gravitatorio. Terence parecerá estar muy arriba en ese campo y, debido a la dilatación del tiempo gravitacional , su reloj parecerá ir más rápido, tanto que el resultado neto será que Terence ha envejecido más que Stella cuando vuelvan a estar juntos. [38] Los argumentos teóricos que predicen la dilatación del tiempo gravitacional no son exclusivos de la relatividad general. Cualquier teoría de la gravedad predecirá la dilatación del tiempo gravitacional si respeta el principio de equivalencia, incluida la teoría de Newton. [3] : 16
Esta sección introductoria se ha centrado en el espacio-tiempo de la relatividad especial, ya que es el más fácil de describir. El espacio-tiempo de Minkowski es plano, no tiene en cuenta la gravedad, es uniforme en todas sus partes y no sirve más que como un fondo estático para los eventos que tienen lugar en él. La presencia de la gravedad complica enormemente la descripción del espacio-tiempo. En la relatividad general, el espacio-tiempo ya no es un fondo estático, sino que interactúa activamente con los sistemas físicos que contiene. El espacio-tiempo se curva en presencia de materia, puede propagar ondas, doblar la luz y exhibe una serie de otros fenómenos. [3] : 221 Algunos de estos fenómenos se describen en las secciones posteriores de este artículo.
Un objetivo básico es poder comparar las mediciones realizadas por observadores en movimiento relativo. Si hay un observador O en el sistema S que ha medido las coordenadas de tiempo y espacio de un evento, asignando a este evento tres coordenadas cartesianas y el tiempo medido en su red de relojes sincronizados ( x , y , z , t ) (ver Fig. 1-1). Un segundo observador O′ en un sistema diferente S′ mide el mismo evento en su sistema de coordenadas y su red de relojes sincronizados ( x ′ , y ′ , z ′ , t ′ ) . Con sistemas inerciales, ninguno de los observadores está bajo aceleración, y un conjunto simple de ecuaciones nos permite relacionar las coordenadas ( x , y , z , t ) con ( x ′ , y ′ , z ′ , t ′ ) . Dado que los dos sistemas de coordenadas están en configuración estándar, es decir, están alineados con coordenadas paralelas ( x , y , z ) y que t = 0 cuando t ′ = 0 , la transformación de coordenadas es la siguiente: [39] [40]
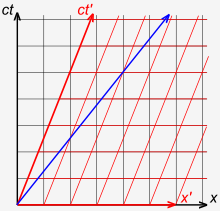
La figura 3-1 ilustra que en la teoría de Newton, el tiempo es universal, no la velocidad de la luz. [41] : 36–37 Considere el siguiente experimento mental: La flecha roja ilustra un tren que se mueve a 0,4 c con respecto a la plataforma. Dentro del tren, un pasajero dispara una bala con una velocidad de 0,4 c en el marco del tren. La flecha azul ilustra que una persona parada en las vías del tren mide la bala como viajando a 0,8 c. Esto está de acuerdo con nuestras expectativas ingenuas.
En términos más generales, suponiendo que el marco S′ se mueve a una velocidad v con respecto al marco S, entonces, dentro del marco S′, el observador O′ mide un objeto que se mueve con velocidad u ′ . La velocidad u con respecto al marco S, dado que x = ut , x ′ = x − vt y t = t ′ , se puede escribir como x ′ = ut − vt = ( u − v ) t = ( u − v ) t ′ . Esto conduce a u ′ = x ′ / t ′ y, en última instancia,
que es la ley galileana de sentido común para la suma de velocidades .

La composición de las velocidades es bastante diferente en el espacio-tiempo relativista. Para reducir ligeramente la complejidad de las ecuaciones, introducimos una abreviatura común para la relación entre la velocidad de un objeto y la de la luz,
La figura 3-2a ilustra un tren rojo que avanza a una velocidad dada por v / c = β = s / a . Desde el marco preparado del tren, un pasajero dispara una bala con una velocidad dada por u ′ / c = β ′ = n / m , donde la distancia se mide a lo largo de una línea paralela al eje x ′ rojo en lugar de paralela al eje x negro . ¿Cuál es la velocidad compuesta u de la bala con respecto a la plataforma, como se representa mediante la flecha azul? Con referencia a la figura 3-2b:
La fórmula relativista para la suma de velocidades presentada anteriormente presenta varias características importantes:

Es fácil obtener expresiones cuantitativas para la dilatación del tiempo y la contracción de la longitud. La figura 3-3 es una imagen compuesta que contiene fotogramas individuales tomados de dos animaciones anteriores, simplificadas y reetiquetadas para los fines de esta sección.
Para reducir ligeramente la complejidad de las ecuaciones, existen distintas notaciones abreviadas para ct :

En la figura 3-3a, los segmentos OA y OK representan intervalos de espacio-tiempo iguales. La dilatación del tiempo está representada por la relación OB / OK . La hipérbola invariante tiene la ecuación w = √ x 2 + k 2 donde k = OK , y la línea roja que representa la línea del universo de una partícula en movimiento tiene la ecuación w = x / β = xc / v . Un poco de manipulación algebraica da como resultado
La expresión que implica el símbolo de la raíz cuadrada aparece muy frecuentemente en relatividad, y una expresión adicional se llama factor de Lorentz, denotado por la letra griega gamma : [42]
Si v es mayor o igual que c , la expresión para pierde todo significado físico, lo que implica que c es la velocidad máxima posible en la naturaleza. Para cualquier v mayor que cero, el factor de Lorentz será mayor que uno, aunque la forma de la curva es tal que para velocidades bajas, el factor de Lorentz es extremadamente cercano a uno.
En la Fig. 3-3b, los segmentos OA y OK representan intervalos de espacio-tiempo iguales. La contracción de longitud está representada por la razón OB / OK . La hipérbola invariante tiene la ecuación x = √ w 2 + k 2 , donde k = OK , y los bordes de la banda azul que representan las líneas del universo de los puntos finales de una varilla en movimiento tienen pendiente 1/ β = c / v . El evento A tiene coordenadas ( x , w ) = ( γk , γβk ). Dado que la línea tangente a través de A y B tiene la ecuación w = ( x − OB )/ β , tenemos γβk = ( γk − OB )/ β y
Las transformaciones de Galileo y su consecuente ley de sentido común de suma de velocidades funcionan bien en nuestro mundo ordinario de baja velocidad de aviones, automóviles y pelotas. Sin embargo, a partir de mediados del siglo XIX, la instrumentación científica sensible comenzó a detectar anomalías que no encajaban bien con la suma ordinaria de velocidades.
Las transformaciones de Lorentz se utilizan para transformar las coordenadas de un evento de un marco a otro en relatividad especial.
El factor de Lorentz aparece en las transformaciones de Lorentz:
Las transformaciones inversas de Lorentz son:
Cuando v ≪ c y x es suficientemente pequeño, los términos v 2 / c 2 y vx / c 2 se acercan a cero, y las transformaciones de Lorentz se aproximan a las transformaciones galileanas.
etc., la mayoría de las veces realmente significan etc. Aunque para abreviar las ecuaciones de transformación de Lorentz se escriben sin deltas, x significa Δ x , etc. En general, siempre nos preocupan las diferencias de espacio y tiempo entre eventos.
Llamar a un conjunto de transformaciones transformaciones normales de Lorentz y al otro transformaciones inversas es engañoso, ya que no hay diferencia intrínseca entre los sistemas de referencia. Diferentes autores llaman a uno u otro conjunto de transformaciones el conjunto "inverso". Las transformaciones hacia delante y hacia atrás están trivialmente relacionadas entre sí, ya que el sistema de referencia S solo puede moverse hacia delante o hacia atrás con respecto a S ′ . Por lo tanto, invertir las ecuaciones simplemente implica intercambiar las variables primadas y no primadas y reemplazar v por − v . [43] : 71–79
Ejemplo: Terence y Stella participan en una carrera espacial de la Tierra a Marte. Terence es un oficial en la línea de partida, mientras que Stella es una participante. En el momento t = t ′ = 0 , la nave espacial de Stella acelera instantáneamente a una velocidad de 0,5 c . La distancia de la Tierra a Marte es de 300 segundos luz (aproximadamente90,0 × 10 6 km ). Terence observa a Stella cruzando el reloj de la línea de meta en t = 600,00 s . Pero Stella observa que el tiempo en el cronómetro de su barco es cuando pasa la línea de meta, y calcula que la distancia entre las líneas de salida y llegada, medida en su marco, es de 259,81 segundos luz (aproximadamente77,9 × 10 6 kilómetros ). 1).
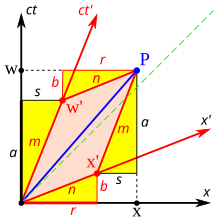
Ha habido muchas docenas de derivaciones de las transformaciones de Lorentz desde el trabajo original de Einstein en 1905, cada una con su enfoque particular. Aunque la derivación de Einstein se basó en la invariancia de la velocidad de la luz, hay otros principios físicos que pueden servir como puntos de partida. En última instancia, estos puntos de partida alternativos pueden considerarse diferentes expresiones del principio subyacente de localidad , que establece que la influencia que una partícula ejerce sobre otra no puede transmitirse instantáneamente. [44]
La derivación dada aquí e ilustrada en la Fig. 3-5 se basa en una presentada por Bais [41] : 64–66 y hace uso de resultados previos de las secciones Composición relativista de velocidades, Dilatación del tiempo y Contracción de longitud. El evento P tiene coordenadas ( w , x ) en el "sistema de reposo" negro y coordenadas ( w ′ , x ′ ) en el marco rojo que se mueve con el parámetro de velocidad β = v / c . Para determinar w ′ y x ′ en términos de w y x (o al revés) es más fácil al principio derivar la transformación inversa de Lorentz.
Las ecuaciones anteriores son expresiones alternativas para las ecuaciones t y x de la transformación inversa de Lorentz, como se puede ver al sustituir ct por w , ct ′ por w ′ y v / c por β . A partir de la transformación inversa, las ecuaciones de la transformación hacia adelante se pueden derivar al resolver para t ′ y x ′ .
Las transformaciones de Lorentz tienen una propiedad matemática llamada linealidad, ya que x ′ y t ′ se obtienen como combinaciones lineales de x y t , sin potencias superiores involucradas. La linealidad de la transformación refleja una propiedad fundamental del espacio-tiempo que se asumió tácitamente en la derivación, a saber, que las propiedades de los marcos de referencia inerciales son independientes de la ubicación y el tiempo. En ausencia de gravedad, el espacio-tiempo parece el mismo en todas partes. [41] : 67 Todos los observadores inerciales estarán de acuerdo en lo que constituye movimiento acelerado y no acelerado. [43] : 72–73 Cualquier observador puede usar sus propias mediciones de espacio y tiempo, pero no hay nada absoluto en ellas. Las convenciones de otro observador funcionarán igual de bien. [3] : 190
Un resultado de la linealidad es que si se aplican secuencialmente dos transformaciones de Lorentz, el resultado también es una transformación de Lorentz.
Ejemplo: Terence observa a Stella alejándose de él a una velocidad de 0,500 c y puede usar las transformaciones de Lorentz con β = 0,500 para relacionar las mediciones de Stella con las suyas. Stella, en su marco, observa a Ursula alejándose de él a una velocidad de 0,250 c y puede usar las transformaciones de Lorentz con β = 0,250 para relacionar las mediciones de Ursula con las suyas. Debido a la linealidad de las transformaciones y a la composición relativista de las velocidades, Terence puede usar las transformaciones de Lorentz con β = 0,666 para relacionar las mediciones de Ursula con las suyas.
El efecto Doppler es el cambio de frecuencia o longitud de onda de una onda para un receptor y una fuente en movimiento relativo. Para simplificar, consideramos aquí dos escenarios básicos: (1) Los movimientos de la fuente y/o el receptor se producen exactamente a lo largo de la línea que los une (efecto Doppler longitudinal), y (2) los movimientos forman ángulos rectos con respecto a dicha línea ( efecto Doppler transversal ). Ignoramos los escenarios en los que se mueven a lo largo de ángulos intermedios.
El análisis Doppler clásico se ocupa de las ondas que se propagan en un medio, como las ondas sonoras o las ondulaciones del agua, y que se transmiten entre fuentes y receptores que se mueven acercándose o alejándose uno del otro. El análisis de dichas ondas depende de si la fuente, el receptor o ambos se mueven en relación con el medio. Dado el escenario en el que el receptor está estacionario con respecto al medio y la fuente se aleja directamente del receptor a una velocidad de v s para un parámetro de velocidad de β s , la longitud de onda aumenta y la frecuencia observada f viene dada por
Por otra parte, dado el escenario donde la fuente es estacionaria y el receptor se está alejando directamente de la fuente a una velocidad de v r para un parámetro de velocidad de β r , la longitud de onda no cambia, pero la velocidad de transmisión de las ondas en relación con el receptor disminuye, y la frecuencia observada f está dada por
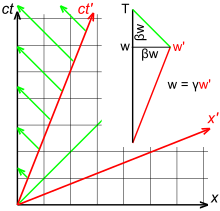
La luz, a diferencia del sonido o las ondas del agua, no se propaga a través de un medio y no hay distinción entre una fuente que se aleja del receptor o un receptor que se aleja de la fuente. La figura 3-6 ilustra un diagrama de espacio-tiempo relativista que muestra una fuente que se separa del receptor con un parámetro de velocidad de modo que la separación entre la fuente y el receptor en el tiempo es . Debido a la dilatación del tiempo, Puesto que la pendiente del rayo de luz verde es −1, Por lo tanto, el efecto Doppler relativista está dado por [41] : 58–59

Supongamos que una fuente y un receptor, que se aproximan entre sí en un movimiento inercial uniforme a lo largo de líneas que no se intersecan, están en su punto más cercano de aproximación entre sí. Parecería que el análisis clásico predice que el receptor no detecta ningún desplazamiento Doppler. Debido a sutilezas en el análisis, esa expectativa no es necesariamente cierta. Sin embargo, cuando se define adecuadamente, el desplazamiento Doppler transversal es un efecto relativista que no tiene análogo clásico. Las sutilezas son las siguientes: [45] : 541–543
En los debates sobre el desplazamiento Doppler transversal se examinan habitualmente otros dos escenarios:
<!—end plainlist—>
In scenario (a), the point of closest approach is frame-independent and represents the moment where there is no change in distance versus time (i.e. dr/dt = 0 where r is the distance between receiver and source) and hence no longitudinal Doppler shift. The source observes the receiver as being illuminated by light of frequency f′, but also observes the receiver as having a time-dilated clock. In frame S, the receiver is therefore illuminated by blueshifted light of frequency
In scenario (b) the illustration shows the receiver being illuminated by light from when the source was closest to the receiver, even though the source has moved on. Because the source's clocks are time dilated as measured in frame S, and since dr/dt was equal to zero at this point, the light from the source, emitted from this closest point, is redshifted with frequency
Scenarios (c) and (d) can be analyzed by simple time dilation arguments. In (c), the receiver observes light from the source as being blueshifted by a factor of , and in (d), the light is redshifted. The only seeming complication is that the orbiting objects are in accelerated motion. However, if an inertial observer looks at an accelerating clock, only the clock's instantaneous speed is important when computing time dilation. (The converse, however, is not true.)[45]: 541–543 Most reports of transverse Doppler shift refer to the effect as a redshift and analyze the effect in terms of scenarios (b) or (d).[note 11]

In classical mechanics, the state of motion of a particle is characterized by its mass and its velocity. Linear momentum, the product of a particle's mass and velocity, is a vector quantity, possessing the same direction as the velocity: p = mv. It is a conserved quantity, meaning that if a closed system is not affected by external forces, its total linear momentum cannot change.
In relativistic mechanics, the momentum vector is extended to four dimensions. Added to the momentum vector is a time component that allows the spacetime momentum vector to transform like the spacetime position vector . In exploring the properties of the spacetime momentum, we start, in Fig. 3-8a, by examining what a particle looks like at rest. In the rest frame, the spatial component of the momentum is zero, i.e. p = 0, but the time component equals mc.
We can obtain the transformed components of this vector in the moving frame by using the Lorentz transformations, or we can read it directly from the figure because we know that and , since the red axes are rescaled by gamma. Fig. 3-8b illustrates the situation as it appears in the moving frame. It is apparent that the space and time components of the four-momentum go to infinity as the velocity of the moving frame approaches c.[41]: 84–87
We will use this information shortly to obtain an expression for the four-momentum.
Light particles, or photons, travel at the speed of c, the constant that is conventionally known as the speed of light. This statement is not a tautology, since many modern formulations of relativity do not start with constant speed of light as a postulate. Photons therefore propagate along a lightlike world line and, in appropriate units, have equal space and time components for every observer.
A consequence of Maxwell's theory of electromagnetism is that light carries energy and momentum, and that their ratio is a constant: . Rearranging, , and since for photons, the space and time components are equal, E/c must therefore be equated with the time component of the spacetime momentum vector.
Photons travel at the speed of light, yet have finite momentum and energy. For this to be so, the mass term in γmc must be zero, meaning that photons are massless particles. Infinity times zero is an ill-defined quantity, but E/c is well-defined.
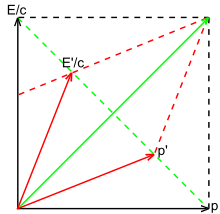
By this analysis, if the energy of a photon equals E in the rest frame, it equals in a moving frame. This result can be derived by inspection of Fig. 3-9 or by application of the Lorentz transformations, and is consistent with the analysis of Doppler effect given previously.[41]: 88
Consideration of the interrelationships between the various components of the relativistic momentum vector led Einstein to several important conclusions.
Another way of looking at the relationship between mass and energy is to consider a series expansion of γmc2 at low velocity:
The second term is just an expression for the kinetic energy of the particle. Mass indeed appears to be another form of energy.[41]: 90–92 [43]: 129–130, 180
The concept of relativistic mass that Einstein introduced in 1905, mrel, although amply validated every day in particle accelerators around the globe (or indeed in any instrumentation whose use depends on high velocity particles, such as electron microscopes,[46] old-fashioned color television sets, etc.), has nevertheless not proven to be a fruitful concept in physics in the sense that it is not a concept that has served as a basis for other theoretical development. Relativistic mass, for instance, plays no role in general relativity.
For this reason, as well as for pedagogical concerns, most physicists currently prefer a different terminology when referring to the relationship between mass and energy.[47] "Relativistic mass" is a deprecated term. The term "mass" by itself refers to the rest mass or invariant mass, and is equal to the invariant length of the relativistic momentum vector. Expressed as a formula,
This formula applies to all particles, massless as well as massive. For photons where mrest equals zero, it yields, .[41]: 90–92
Because of the close relationship between mass and energy, the four-momentum (also called 4-momentum) is also called the energy–momentum 4-vector. Using an uppercase P to represent the four-momentum and a lowercase p to denote the spatial momentum, the four-momentum may be written as
In physics, conservation laws state that certain particular measurable properties of an isolated physical system do not change as the system evolves over time. In 1915, Emmy Noether discovered that underlying each conservation law is a fundamental symmetry of nature.[48] The fact that physical processes do not care where in space they take place (space translation symmetry) yields conservation of momentum, the fact that such processes do not care when they take place (time translation symmetry) yields conservation of energy, and so on. In this section, we examine the Newtonian views of conservation of mass, momentum and energy from a relativistic perspective.
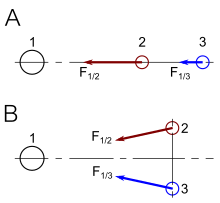
To understand how the Newtonian view of conservation of momentum needs to be modified in a relativistic context, we examine the problem of two colliding bodies limited to a single dimension.
In Newtonian mechanics, two extreme cases of this problem may be distinguished yielding mathematics of minimum complexity:
For both cases (1) and (2), momentum, mass, and total energy are conserved. However, kinetic energy is not conserved in cases of inelastic collision. A certain fraction of the initial kinetic energy is converted to heat.
In case (2), two masses with momentums and collide to produce a single particle of conserved mass traveling at the center of mass velocity of the original system, . The total momentum is conserved.
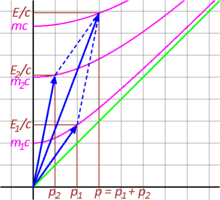
Fig. 3-10 illustrates the inelastic collision of two particles from a relativistic perspective. The time components and add up to total E/c of the resultant vector, meaning that energy is conserved. Likewise, the space components and add up to form p of the resultant vector. The four-momentum is, as expected, a conserved quantity. However, the invariant mass of the fused particle, given by the point where the invariant hyperbola of the total momentum intersects the energy axis, is not equal to the sum of the invariant masses of the individual particles that collided. Indeed, it is larger than the sum of the individual masses: .[41]: 94–97
Looking at the events of this scenario in reverse sequence, we see that non-conservation of mass is a common occurrence: when an unstable elementary particle spontaneously decays into two lighter particles, total energy is conserved, but the mass is not. Part of the mass is converted into kinetic energy.[43]: 134–138
The freedom to choose any frame in which to perform an analysis allows us to pick one which may be particularly convenient. For analysis of momentum and energy problems, the most convenient frame is usually the "center-of-momentum frame" (also called the zero-momentum frame, or COM frame). This is the frame in which the space component of the system's total momentum is zero. Fig. 3-11 illustrates the breakup of a high speed particle into two daughter particles. In the lab frame, the daughter particles are preferentially emitted in a direction oriented along the original particle's trajectory. In the COM frame, however, the two daughter particles are emitted in opposite directions, although their masses and the magnitude of their velocities are generally not the same.[49]
In a Newtonian analysis of interacting particles, transformation between frames is simple because all that is necessary is to apply the Galilean transformation to all velocities. Since , the momentum . If the total momentum of an interacting system of particles is observed to be conserved in one frame, it will likewise be observed to be conserved in any other frame.[43]: 241–245
Conservation of momentum in the COM frame amounts to the requirement that p = 0 both before and after collision. In the Newtonian analysis, conservation of mass dictates that . In the simplified, one-dimensional scenarios that we have been considering, only one additional constraint is necessary before the outgoing momenta of the particles can be determined—an energy condition. In the one-dimensional case of a completely elastic collision with no loss of kinetic energy, the outgoing velocities of the rebounding particles in the COM frame will be precisely equal and opposite to their incoming velocities. In the case of a completely inelastic collision with total loss of kinetic energy, the outgoing velocities of the rebounding particles will be zero.[43]: 241–245
Newtonian momenta, calculated as , fail to behave properly under Lorentzian transformation. The linear transformation of velocities is replaced by the highly nonlinear so that a calculation demonstrating conservation of momentum in one frame will be invalid in other frames. Einstein was faced with either having to give up conservation of momentum, or to change the definition of momentum. This second option was what he chose.[41]: 104
The relativistic conservation law for energy and momentum replaces the three classical conservation laws for energy, momentum and mass. Mass is no longer conserved independently, because it has been subsumed into the total relativistic energy. This makes the relativistic conservation of energy a simpler concept than in nonrelativistic mechanics, because the total energy is conserved without any qualifications. Kinetic energy converted into heat or internal potential energy shows up as an increase in mass.[43]: 127
Fig. 3-12a illustrates the energy–momentum diagram for this decay reaction in the rest frame of the pion. Because of its negligible mass, a neutrino travels at very nearly the speed of light. The relativistic expression for its energy, like that of the photon, is which is also the value of the space component of its momentum. To conserve momentum, the muon has the same value of the space component of the neutrino's momentum, but in the opposite direction.
Algebraic analyses of the energetics of this decay reaction are available online,[50] so Fig. 3-12b presents instead a graphing calculator solution. The energy of the neutrino is 29.79 MeV, and the energy of the muon is 33.91 MeV − 29.79 MeV = 4.12 MeV. Most of the energy is carried off by the near-zero-mass neutrino.Newton's theories assumed that motion takes place against the backdrop of a rigid Euclidean reference frame that extends throughout all space and all time. Gravity is mediated by a mysterious force, acting instantaneously across a distance, whose actions are independent of the intervening space.[note 12] In contrast, Einstein denied that there is any background Euclidean reference frame that extends throughout space. Nor is there any such thing as a force of gravitation, only the structure of spacetime itself.[51]: 175–190
In spacetime terms, the path of a satellite orbiting the Earth is not dictated by the distant influences of the Earth, Moon and Sun. Instead, the satellite moves through space only in response to local conditions. Since spacetime is everywhere locally flat when considered on a sufficiently small scale, the satellite is always following a straight line in its local inertial frame. We say that the satellite always follows along the path of a geodesic. No evidence of gravitation can be discovered following alongside the motions of a single particle.[51]: 175–190
In any analysis of spacetime, evidence of gravitation requires that one observe the relative accelerations of two bodies or two separated particles. In Fig. 5-1, two separated particles, free-falling in the gravitational field of the Earth, exhibit tidal accelerations due to local inhomogeneities in the gravitational field such that each particle follows a different path through spacetime. The tidal accelerations that these particles exhibit with respect to each other do not require forces for their explanation. Rather, Einstein described them in terms of the geometry of spacetime, i.e. the curvature of spacetime. These tidal accelerations are strictly local. It is the cumulative total effect of many local manifestations of curvature that result in the appearance of a gravitational force acting at a long range from Earth.[51]: 175–190
Two central propositions underlie general relativity.

In Poincaré's conventionalist views, the essential criteria according to which one should select a Euclidean versus non-Euclidean geometry would be economy and simplicity. A realist would say that Einstein discovered spacetime to be non-Euclidean. A conventionalist would say that Einstein merely found it more convenient to use non-Euclidean geometry. The conventionalist would maintain that Einstein's analysis said nothing about what the geometry of spacetime really is.[55]
Such being said,
In response to the first question, a number of authors including Deser, Grishchuk, Rosen, Weinberg, etc. have provided various formulations of gravitation as a field in a flat manifold. Those theories are variously called "bimetric gravity", the "field-theoretical approach to general relativity", and so forth.[56][57][58][59] Kip Thorne has provided a popular review of these theories.[60]: 397–403
The flat spacetime paradigm posits that matter creates a gravitational field that causes rulers to shrink when they are turned from circumferential orientation to radial, and that causes the ticking rates of clocks to dilate. The flat spacetime paradigm is fully equivalent to the curved spacetime paradigm in that they both represent the same physical phenomena. However, their mathematical formulations are entirely different. Working physicists routinely switch between using curved and flat spacetime techniques depending on the requirements of the problem. The flat spacetime paradigm is convenient when performing approximate calculations in weak fields. Hence, flat spacetime techniques tend be used when solving gravitational wave problems, while curved spacetime techniques tend be used in the analysis of black holes.[60]: 397–403
The spacetime symmetry group for Special Relativity is the Poincaré group, which is a ten-dimensional group of three Lorentz boosts, three rotations, and four spacetime translations. It is logical to ask what symmetries if any might apply in General Relativity. A tractable case might be to consider the symmetries of spacetime as seen by observers located far away from all sources of the gravitational field. The naive expectation for asymptotically flat spacetime symmetries might be simply to extend and reproduce the symmetries of flat spacetime of special relativity, viz., the Poincaré group.
In 1962 Hermann Bondi, M. G. van der Burg, A. W. Metzner[61] and Rainer K. Sachs[62] addressed this asymptotic symmetry problem in order to investigate the flow of energy at infinity due to propagating gravitational waves. Their first step was to decide on some physically sensible boundary conditions to place on the gravitational field at lightlike infinity to characterize what it means to say a metric is asymptotically flat, making no a priori assumptions about the nature of the asymptotic symmetry group—not even the assumption that such a group exists. Then after designing what they considered to be the most sensible boundary conditions, they investigated the nature of the resulting asymptotic symmetry transformations that leave invariant the form of the boundary conditions appropriate for asymptotically flat gravitational fields.[63]: 35
What they found was that the asymptotic symmetry transformations actually do form a group and the structure of this group does not depend on the particular gravitational field that happens to be present. This means that, as expected, one can separate the kinematics of spacetime from the dynamics of the gravitational field at least at spatial infinity. The puzzling surprise in 1962 was their discovery of a rich infinite-dimensional group (the so-called BMS group) as the asymptotic symmetry group, instead of the finite-dimensional Poincaré group, which is a subgroup of the BMS group. Not only are the Lorentz transformations asymptotic symmetry transformations, there are also additional transformations that are not Lorentz transformations but are asymptotic symmetry transformations. In fact, they found an additional infinity of transformation generators known as supertranslations. This implies the conclusion that General Relativity (GR) does not reduce to special relativity in the case of weak fields at long distances.[63]: 35
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric (an inner product on the tangent space at each point that varies smoothly from point to point). This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
Riemannian geometry originated with the vision of Bernhard Riemann expressed in his inaugural lecture "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen" ("On the Hypotheses on which Geometry is Based").[64] It is a very broad and abstract generalization of the differential geometry of surfaces in R3. Development of Riemannian geometry resulted in synthesis of diverse results concerning the geometry of surfaces and the behavior of geodesics on them, with techniques that can be applied to the study of differentiable manifolds of higher dimensions. It enabled the formulation of Einstein's general theory of relativity, made profound impact on group theory and representation theory, as well as analysis, and spurred the development of algebraic and differential topology.For physical reasons, a spacetime continuum is mathematically defined as a four-dimensional, smooth, connected Lorentzian manifold . This means the smooth Lorentz metric has signature . The metric determines the geometry of spacetime, as well as determining the geodesics of particles and light beams. About each point (event) on this manifold, coordinate charts are used to represent observers in reference frames. Usually, Cartesian coordinates are used. Moreover, for simplicity's sake, units of measurement are usually chosen such that the speed of light is equal to 1.[65]
A reference frame (observer) can be identified with one of these coordinate charts; any such observer can describe any event . Another reference frame may be identified by a second coordinate chart about . Two observers (one in each reference frame) may describe the same event but obtain different descriptions.[65]
Usually, many overlapping coordinate charts are needed to cover a manifold. Given two coordinate charts, one containing (representing an observer) and another containing (representing another observer), the intersection of the charts represents the region of spacetime in which both observers can measure physical quantities and hence compare results. The relation between the two sets of measurements is given by a non-singular coordinate transformation on this intersection. The idea of coordinate charts as local observers who can perform measurements in their vicinity also makes good physical sense, as this is how one actually collects physical data—locally.[65]
For example, two observers, one of whom is on Earth, but the other one who is on a fast rocket to Jupiter, may observe a comet crashing into Jupiter (this is the event ). In general, they will disagree about the exact location and timing of this impact, i.e., they will have different 4-tuples (as they are using different coordinate systems). Although their kinematic descriptions will differ, dynamical (physical) laws, such as momentum conservation and the first law of thermodynamics, will still hold. In fact, relativity theory requires more than this in the sense that it stipulates these (and all other physical) laws must take the same form in all coordinate systems. This introduces tensors into relativity, by which all physical quantities are represented.
Geodesics are said to be timelike, null, or spacelike if the tangent vector to one point of the geodesic is of this nature. Paths of particles and light beams in spacetime are represented by timelike and null (lightlike) geodesics, respectively.[65]
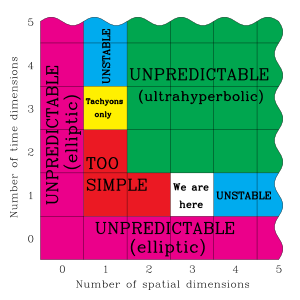
There are two kinds of dimensions: spatial (bidirectional) and temporal (unidirectional).[67] Let the number of spatial dimensions be N and the number of temporal dimensions be T. That N = 3 and T = 1, setting aside the compactified dimensions invoked by string theory and undetectable to date, can be explained by appealing to the physical consequences of letting N differ from 3 and T differ from 1. The argument is often of an anthropic character and possibly the first of its kind, albeit before the complete concept came into vogue.
The implicit notion that the dimensionality of the universe is special is first attributed to Gottfried Wilhelm Leibniz, who in the Discourse on Metaphysics suggested that the world is "the one which is at the same time the simplest in hypothesis and the richest in phenomena".[68] Immanuel Kant argued that 3-dimensional space was a consequence of the inverse square law of universal gravitation. While Kant's argument is historically important, John D. Barrow said that it "gets the punch-line back to front: it is the three-dimensionality of space that explains why we see inverse-square force laws in Nature, not vice-versa" (Barrow 2002:204).[note 13]
In 1920, Paul Ehrenfest showed that if there is only a single time dimension and more than three spatial dimensions, the orbit of a planet about its Sun cannot remain stable. The same is true of a star's orbit around the center of its galaxy.[69] Ehrenfest also showed that if there are an even number of spatial dimensions, then the different parts of a wave impulse will travel at different speeds. If there are spatial dimensions, where k is a positive whole number, then wave impulses become distorted. In 1922, Hermann Weyl claimed that Maxwell's theory of electromagnetism can be expressed in terms of an action only for a four-dimensional manifold.[70] Finally, Tangherlini showed in 1963 that when there are more than three spatial dimensions, electron orbitals around nuclei cannot be stable; electrons would either fall into the nucleus or disperse.[71]
Max Tegmark expands on the preceding argument in the following anthropic manner.[72] If T differs from 1, the behavior of physical systems could not be predicted reliably from knowledge of the relevant partial differential equations. In such a universe, intelligent life capable of manipulating technology could not emerge. Moreover, if T > 1, Tegmark maintains that protons and electrons would be unstable and could decay into particles having greater mass than themselves. (This is not a problem if the particles have a sufficiently low temperature.)[72] Lastly, if N < 3, gravitation of any kind becomes problematic, and the universe would probably be too simple to contain observers. For example, when N < 3, nerves cannot cross without intersecting.[72] Hence anthropic and other arguments rule out all cases except N = 3 and T = 1, which describes the world around us.
On the other hand, in view of creating black holes from an ideal monatomic gas under its self-gravity, Wei-Xiang Feng showed that (3 + 1)-dimensional spacetime is the marginal dimensionality. Moreover, it is the unique dimensionality that can afford a "stable" gas sphere with a "positive" cosmological constant. However, a self-gravitating gas cannot be stably bound if the mass sphere is larger than ~1021 solar masses, due to the small positivity of the cosmological constant observed.[73]
In 2019, James Scargill argued that complex life may be possible with two spatial dimensions. According to Scargill, a purely scalar theory of gravity may enable a local gravitational force, and 2D networks may be sufficient for complex neural networks.[74][75]{{cite book}}: CS1 maint: location missing publisher (link)...redacted transcript of a course given by the author at Harvard in spring semester 2016. It contains a pedagogical overview of recent developments connecting the subjects of soft theorems, the memory effect and asymptotic symmetries in four-dimensional QED, nonabelian gauge theory and gravity with applications to black holes. To be published Princeton University Press, 158 pages.